|
|
By Joselle, on May 21st, 2012 The extent to which an idea in mathematics creates an idea in science is largely underappreciated. It is common to think of mathematics as the tool that one needs to describe the reality explored by physics, as if the mathematics is secondary, or a purely linguistic consideration. But it should be clear that this is only part of the story. The bigger story is highlighted by yet another article I read today about a Foundational Institute award recipient whose work is focused on uniting quantum mechanics and general relativity (as is Bob Coecke’s work, who is also supported by the Institute, and was the subject of my last post). This awardee is David Rideout, a physicist at the University of California, San Diego and his ideas have their seeds in the transformational insights of Riemann.
The fabric of space-time, as it is now understood, breaks down inside a black hole, where huge masses are confined to very small regions creating points of inconceivably infinite density. Another kind of infinity plagues quantum theory. Rafael Sorkin, a physicist at Syracuse University, New York adds that, “The bare electric charge of the electron is very badly infinite” in the quantum equations of electromagnetic force, a fact not reflected in reality. Rideout and others have considered that a way around these difficulties is to imagine space-time as a network of discrete chunks rather than as a continuous fabric. The chunks are very small, a mere 10 to the minus 35 meters across. But in this world, space-time could never shrink to the infinitely small volumes that the mathematics of black holes has to deal with, because there would no longer be the continuity that produces them. To keep this world from being just a “pile of dust,” in contrast to our dynamic universe, this discreteness would have to be combined with causal structure. It turns out that this combination of attributes can be found in an area of mathematics called causal set theory. The hope is to build space-time out of related but discrete pieces.
The project goes like this: Start with a list of every point in space and time, all the way back to the Big Bang. Then add information about the relationship between every pair of points in the set. Luckily, there is only one thing you need to know about the relationship between those two points: Can A affect B? Thanks to Einstein’s theory of special relativity, we know that nothing can travel faster than the speed of light. This means that some pairs of points in space-time will be forever disconnected. So, if the two points are suitably distant in time and space, the answer will be no, one could not have affected the other. If they are close enough, the answer is yes. A causal set is a roster of those “no” and “yes” answers for every pair of points in space and time.
Rideout belief is this,
that causal sets offer a view of time as a process that is occurring—as in quantum theory—with the future being formed as we live our lives and make decisions: “The growth dynamics of causal sets expresses the progression of time as a continual process of becoming, like the unfolding of a flower or the growth of a tree.”
Einstein Online does a really nice job of describing how this ordering brings about a geometry, tracing the idea of discrete space back to Zeno as well as Riemann’s famous 1854 lecture. In this lecture, Riemann addressed the foundations of geometry with a careful scrutiny of the notions: number, magnitude, and manifold. Riemann is quoted in the Einstein Online discussion saying:
“The question of the validity of the presuppositions of geometry in the infinitely small hangs together with the question of the inner ground of the metric relationships of space. In connection with the latter question… the above remark applies, that for a discrete manifold, the principle of its metric relationships is already contained in the concept of the manifold itself, whereas for a continuous manifold, it must come from somewhere else. Therefore, either the reality which underlies physical space must form a discrete manifold or else the basis of its metric relationships should be sought for outside it[…].”
Here Riemann is asking what it is about the structure of space that makes it possible to talk about measurable things like distance, area, volume and angles (the “metric relationships”), and he is contrasting the case in which the deep structure of space is continuous with the case in which it is discrete. In a continuous space (like that of Euclidean geometry) there are between any two points always an infinity of others, and every volume can be divided into smaller and smaller volumes without limit. In a discrete space, in contrast, any bounded region is composed of a finite number of elements or “building blocks”, and the process of subdivision must always come to an end at some stage. Riemann’s point, then, is that a discrete space has metric information built in from the start. It is easy to see the truth of this: For instance, simply counting the elements composing a region of space provides a natural measure of that region’s volume. For a continuous space, in contrast, this possibility to count elements is lacking (you’d just get infinity for the answer) and the origin of the metric relationships has to be explained in some other manner.”
Einstein borrowed Riemann’s notion of a continuous curved space for his theory of general relativity but also foresaw Riemann’s discrete space possibility, renaming Riemann’s discrete manifold a continuum-discontinuum. This quote from Einstein was also provided by Einstein Online (from a published 1954 letter):
“In any case, it seems to me that the alternative continuum-discontinuum is a genuine alternative; i.e. there is no compromise here. In [a discontinuum] theory there cannot be space and time, only numbers[…]. It will be especially difficult to elicit something like a spatio-temporal quasi-order from such a schema. I can not picture to myself how the axiomatic framework of such a physics could look[…]. But I hold it as altogether possible that developments will lead there[…].”
The apparent simplicity of causal set relationships is impressive. In the space-time continuum there is an elaborate mathematical web of point-events that carry information about smoothness, nearness, times, and distances. But the ordering of the elements of a causal set is much simpler, relying largely on a kind of before or after relationship among the elements. Einstein Online writes the slogan Order + Number = Geometry.
Mathematics is the endless penetration of what order, number, and spatial representations can bring to mind. It’s as if it unleashes the inexhaustible powers of cognition, or the baffling reach of our complex nervous system. When I imagine the mind’s movement – from counting, to its reluctance to accept the square root of 2 as a number, to its conflict over infinities and continuums, to its arithmetization of the limit, then finding a generalized notion of space, that later brings it back to counting – it looks like one of the major waterways moving through our water driven planet.
By Joselle, on May 8th, 2012 Bob Coecke has received a grant of over $111,000 from the Foundational Questions Institute to continue his work on a graphical language to describe quantum mechanical processes. The work is based on category theory, a branch of mathematics that focuses less on the mathematical objects themselves, and more on the maps that transform them. The institute has an article on his work here.
The quantum mechanical world of subatomic particles is conceptually difficult. There is little dispute over the validity of the mathematical description of this world. It has a highly precise predictive value. But the mathematical grasp of this reality deviates from our experience more than any of the previous models of our universe which physics has proposed. As I heard Frank Wilczek once say, in the quantum mechanical world empty space is a turbulent medium of fluctuations, of particles that come to be and pass away.
We all have difficulty seeing this world, not because the mathematics is complex (although it is), but because we can’t quite grasp what the mathematics seems to be telling us. There is still disagreement among physicists about whether the wave function, the mathematical object that determines the probability of different outcomes of measurements, reflects the incomplete knowledge of an experimenter, or actually tells us that the state of a physical system is never one way or another. The other fairly popularized problem in physics is the incompatibility of quantum mechanics with general relativity.
Our description of the tiniest reality creates a problem for our description of the really large one. Since it is the mathematics that seems to have created the difficulties, the hope for resolution is in mathematics as well. String Theory is one of these hopes.
But I was struck today by what category theory has to offer, and I became interested particularly because category theory is a shift from objects to processes and is yet another level of abstraction.
Category theory began as a study of the processes that exist in mathematics and then became a mathematical subject in its own right. A category is a collection of objects together with what one would call the structure preserving maps that exist between them, like a function that turns real numbers into other real numbers. Since category theory doesn’t depend on other mathematics, it can be used as the foundational structure of the discipline (an alternative to set theory). Its advantage is that it provides for the discussion of the properties of maps in the abstract. Maps are actions more than things. In their abstraction, the maps are sometimes called arrows (and in diagrams they are arrows). About the graphical scheme that he uses, Coecke says that it’s a much more natural way to write things.
That means you can go on to describe the relations between different, and complicated, quantum processes in a clear and simple way—an especially useful trick when you want to represent some of the strange features of quantum theory, such as entanglement, nonlocality and teleportation.
The processes are represented by boxes and their interaction by wires between them.
The diagrams provide a clear, visual way to see at a glance how things change in a system, as time progresses across the diagram, depicted by the changing connectivity of the boxes. Difficult quantum calculations can be reduced to simple changes to the picture, retaining quantitative information.
To understand the advantage of the scheme, Coecke refers to a common example encountered by computer programmers. “If someone gave you a computer program written in zeroes and ones, there’s no way you could see what it does,” he notes. But if, instead, someone gave you a pictorial flow chart representing the algorithm you are hoping to recreate, you would immediately understand what the program does. “For us, these diagrams are a high-level language to reason about physics,” says Coecke.
Some physicists are optimistic that these alternative representations may also help reconcile quantum theory with general relativity by contributing to a quantum theory of gravity. But, in keeping with the theme of this site, it’s worth noting that Coecke’s scheme can be used to analyze word and sentence meaning, to get at something that language is doing.
Surprisingly, the way words interact to make up a sentence is similar to the way quantum processes interact. Google takes no notice of the order of words on a page, but actually the ordering can completely change a sentence’s meaning. Coecke has used his graphical approach to connect individual words in a sentence so their meaning can be extracted according to both the content of each word and its positioning. This is quite an achievement: most models of human language either focus on individual words or grammatical rules, not both. “Our categorical model blows away the existing language processing models,” says Coecke.
The author of the article, Sophie Hebden, makes an important observation:
The fact that Coecke’s high-level approach to understanding quantum information has such power when applied to other diverse fields, including linguistics, may point to a higher truth: that there are structures common to all layers of reality.
But I would also add the following: It’s significant, I think, that what may be this ‘higher truth’ is brought to light when the mathematics focuses on process rather than object. And this is particularly interesting if we agree to see cognition itself as biologists Maturanna and Varela see it, “not as a representation of the world “out there,” but rather as an ongoing bringing forth of a world through the process of living itself.” While these new worlds are being detected by the very creative use various instruments (our extended senses), they can’t be given shape without mathematics.
By Joselle, on April 30th, 2012 It seems that quite a number of categorical remarks got thrown around by Lawrence Krauss – about philosophers, theologians and physicists – in the discussions surrounding his recent book A Universe From Nothing.
But, as is often the case, these kinds of categorical judgments, that question the value of very different kinds of work, do more to obscure things rather than clarify them. One of the intentions of Krauss’ most recent book (and a goal shared by many popular books about physics) is to bring something particularly surprising, and perhaps conceptually difficult, to the attention of a popular audience – something that will capture their imagination and make them interested. In an interview for the Atlantic, (which may have been motivated by some of the anger surrounding the book) Krauss describes one of the surprises that physics provides:
What’s amazing to me is that we’re now at a point where we can plausibly argue that a universe full of stuff came from a very simple beginning, the simplest of all beginnings: nothing. That’s been driven by profound revolutions in our understanding of the universe, and that seemed to me to be something worth celebrating, and so what I wanted to do was use this question to get people to face this remarkable universe that we live in.
That it’s possible to create particles from no particles is remarkable—that you can do that with impunity, without violating the conservation of energy and all that, is a remarkable thing. The fact that “nothing,” namely empty space, is unstable is amazing. But I’ll be the first to say that empty space as I’m describing it isn’t necessarily nothing, although I will add that it was plenty good enough for Augustine and the people who wrote the Bible. For them an eternal empty void was the definition of nothing, and certainly I show that that kind of nothing ain’t nothing anymore.
The book’s afterward by David Dawkins contributes to some of the anger surrounding its reception. Dawkins writes “Even the last remaining trump card of the theologian, ‘Why is there something rather than nothing?’ shrivels up before your eyes as you read these pages.” A recent review by Columbia professor of philosophy David Albert, appeared in the New York Times, and fueled a controversy. While Krauss responds to these criticisms in the Atlantic interview, he also fans the fire with comments like this one:
Philosophy is a field that, unfortunately, reminds me of that old Woody Allen joke, “those that can’t do, teach, and those that can’t teach, teach gym.” And the worst part of philosophy is the philosophy of science; the only people, as far as I can tell, that read work by philosophers of science are other philosophers of science. It has no impact on physics what so ever, and I doubt that other philosophers read it because it’s fairly technical. And so it’s really hard to understand what justifies it.
Science writer John Horgan has his own take on what he calls “Krauss’ derivative book” and expresses it at the Scientific American blog site.
Whaaaa…??!! Dawkins is comparing the most enduringly profound scientific treatise in history to a pop-science book that recycles a bunch of stale ideas from physics and cosmology. This absurd hyperbole says less about the merits of Krauss’s derivative book than it does about the judgment-impairing intensity of Dawkins’s hatred of religion.
But even-handed physicist Sean Carrol does a really nice job of discussing the relevant science on the Discover Magazine website and adds this useful admonition near the end:
Like most scientists, Lawrence doesn’t get a lot out of the philosophy of science. That’s okay; the point of philosophy is not to be “useful” to science, any more than the point of mycology is to be “useful” to fungi. Philosophers of science aren’t trying to do science, they are trying to understand how science works, and how it should work, and to tease out the logic and standards underlying scientific argumentation, and to situate scientific knowledge within a broader epistemological context, and a bunch of other things that can be perfectly interesting without pretending to be science itself.
For the physicist, the often bewildering nature of our reality is built with experimental data. This ‘nothing’ that is being debated is not a conceptual nothing. But the universe that this data may be revealing, is only possible with the conceptual structures of mathematics. That modern physics, relying so heavily on the purely conceptual science of mathematics, produces these counter-intuitive pictures of the universe, has long inspired me to carefully reflect on the nature of knowing itself. Related to this is exploring what mathematics may be able to show us about cognition (what I try to do with this blog). I’m interested in coming to terms with the reality described by modern physics, especially when cognition is viewed, as biologists Maturana and Varela suggest – not as a representation of the world “out there,” but rather as an ongoing bringing forth of a world through the process of living itself.
I hope that the antagonism between philosophy and science, or the combative tone of the debate between science and religion, will one day quiet down. It seems clear that the ancient source of religious and mystical views lies in the intuition that what we see is not really what’s there. And this is more a hunch about us. The corruption of this honest intuition, by some of the harmful dogma that has grown out of it, is a secondary issue that cannot be corrected by appealing only to science. But science can contribute to the original hunch. It also seems very likely to me that the seeds of new paradigms, yet to develop, may lay dormant in the historical work of people like Schopenhauer.
There is hope for mending some of the schisms, exemplified by the work of the scientists that created The Foundational Questions Institute. Along with some other questions, they put these forward in a statement about their scope and impetus:
- What distinguishes the future from the past, if the universe is governed by physical laws that make no such distinction? How does duration, which we experience, relate to the time described by physics and mathematics?
- What is the relationship between physics, mathematics and information? What determines what exists? How “real” is the world of mathematics—and how “real” is the world of matter?
- Why does the universe seem so complex, given its simple initial conditions, and the elegant mathematics that describes it? Is life ubiquitous in the universe (or beyond)? How does matter give rise to consciousness—or does it?
And they rightly conclude:
Questions like these lie at the frontier of science and at the foundation of our understanding of the universe, and intimately connect with and inform not just scientific fields, but also philosophy, theology and religious belief systems. Answers to these questions will have profound intellectual, practical, and spiritual implications for anyone with deep curiosity about the world’s true nature.
By Joselle, on April 23rd, 2012 I’ve spent a considerable amount of time thinking about how, if mathematics grows out of fundamental cognitive mechanisms, it provides opportunities for seeing more. It is mathematics that allows for the tremendous expansion of empirical study – what we call science. I had the opportunity, last week, to listen to a talk given by Craig Hogan, Director of the Fermilab Center for Particle Astrophysics. Professor Hogan developed his talk around the idea that space-time is not only the stage on which the atoms of the world play, but an active and dynamic entity on its own, and now within reach of systematic study. I was quickly taken by the idea that we are beginning to look at what we live within. This is only possible through the combined productivity of existing models of the universe (requiring the stability of conceived mathematical structures) and herculean attempts at measurement.
Professor Hogan introduced his discussion with the statement that 95% of the matter of the universe does not interact with light. So we can’t see it. The promise of new experiments lies in the detection of gravitational waves that distort space-time in a way, as Hogan suggested, analogous to how sound waves distort air. Hence the title given his talk – Sounds of Space and Time.
In an article for The Observer, the hopes and the motivation for some of this work are discussed.
It is a startling paradox. Harald Lück, a scientist at Geo600, explained: “In his general theory of relativity, Einstein predicted the existence of gravitational waves, which he said would be set off by highly energetic events objects like supernovae or neutron star collisions. However, he also predicted we would never be able to observe these waves because they would be too weak to be detected by the time they reached Earth. We intend to prove him right in the first instance and wrong in the second.
The detection of effects other than the ones we see could provide a vast new territory to explore.
We are going to create a new kind of astronomy,” said Professor Jim Hough, the Glasgow physicist who leads Britain’s contribution to Geo600. “Until now, everything we have learned about the universe has been based on studies of electromagnetic radiation – from infrared to visible light to gamma ray detection. Gravity waves will create a completely new type of astronomy.
The model that shapes these investigations is the curved space-time of relativity, which rests heavily on the modern idea of a curved manifold in mathematics. But the hope of measuring a ripple in the curved space of our universe, caused by an extremely energetic astronomical event (like neutron stars colliding) was once thought outside the range of perceptible effects. I find it astonishing that technology could advance to the point that, by harnessing what we do understand of the physics of our world, instruments can be built to handle these impossible feats. This is a fact of particle physics research as well.
But this shift from light-driven perception to a kind of vibrational-driven perception, as I think about it, corresponds loosely to the current understanding in cognitive science that the body perceives cross modally, through the nervous system’s interconnectivity. My own inclination is to say that, if we take into account the laboriously constructed mathematical relationships that build these empirical possibilities, perhaps the correspondence can even be tightened. Mathematics builds conceptual possibilities using perceived relationships (of things like space and quantity) and linguistic actions like logic and metaphor. I discussed this a bit, with respect to Riemann in particular, in an earlier post. In a paper I read recently, whose purpose is to debunk simplistic and categorical brain-based ideas about how we learn, John Geake of Oxford points to the work of Charles Scott Sherrington who, in 1938, made the following observation of human cognition:
The naive observer would have expected evolution in its course to have supplied us with more various sense organs for ampler perception of the world . . .Not new senses but better liaison between the old senses is what the developing nervous system has in this respect stood for.
I found one of Geake’s references particularly interesting. In congenitally blind children, the abstractions of Braille acquire meaning through the work of the same visual cortices that are active in sighted children when they learn a written language.
To emphasize the cross-modal nature of sensory experience, Kayser (2007) writes that: ‘the brain sees with its ears and touch, and hears with its eyes.’ Moreover, as primates, we are predominantly processors of visual information. This is true even for congenitally blind children who instantiate Braille not in the kinaesthetic areas of their brains, but in those parts of their visual cortices that sighted children dedicate to learning written language. Moreover, unsighted people create the same mental spatial maps of their physical reality as sighted people do (Kriegseis et al. in press). Obviously the information to create spatial maps by blind people comes from auditory and tactile inputs, but it gets used as though it was visual.
Input information is abstracted to be processed and learned, mostly unconsciously, through the brain’s interconnectivity (Dehaene, Kerszberg, and Changeux 1998). Actually, we don’t even create sensory perception in our sensory cortices:
For a long time it was thought that the primary sensory areas are the substrate of our perception. . . . these zones simply generate representational maps of the sensorial information. . .although these respond to stimuli, they are not responsible for . . . perceptions . . . Perceptual experience occurs in certain zones of the frontal lobes [where] neurons combine sensory information with memory information. (Trujillo 2006, M9)
Can it be said that mathematics is fundamentally motivated by the quest for new perceptual experience? In a brief presentation on Penrose tiling, mathematician John Hunton proposes that “Science can’t see what it doesn’t have the language to describe.”
By Joselle, on April 17th, 2012 On April 16 Scientificamerican.com reported on research that links hunting for words with foraging for food.
Our brains may have evolved to forage for some kinds of memories in the same way, shifting our attention from one cluster of stored information to another depending on what each patch has to offer. Recently, Thomas Hills of the University of Warwick in England and his colleagues found experimental evidence for this potential parallel. “Memory foraging” is only one way of thinking about memory—and it does not apply universally to all types of information retained in the brain—but, so far, the analogy seems to work well for particular cases of active remembering.
The report describes how researchers led by Thomas Hills of the University of Warwick used verbal theme clusters to investigate the possibility that the body (or the brain) searches for information in much the same way that a creature searches for food. They used something called verbal fluency, tasks that have been designed to study memory and to test for the breakdown of memory from diseases. It has often been observed that when people are asked to name members of a category (like animals, vegetables, or movies) their lists develop in clusters of related items. In naming animals, for example, when a subcategory is exhausted (like animals that can be pets) they move to another subcategory (like large predators, or ocean animals, etc). The question researchers were trying to answer was whether the moves among subcategories were analogous to the moves an animal might make among food sources. Biologists have mathematical models that describe optimal foraging, and these was used to write software that would characterize the shifts among themed clusters that were made by participants in the study.
Hills coded a computer program that first decided the probability that a student would name a particular animal, given what the student had already named. If someone started with “cat,” for instance, they are much more likely to next type “dog” than “zebra.” When the program encountered a pair of words that were unlikely to appear together, followed by a pair of words with a much higher chance of coupling, it interpreted the pattern as a jump from one themed cluster to another—such as from pets to savanna.
Then the program compared the responses of participants to what optimal foraging models predict. The students whose mental activity most closely matched the model were actually the ones who made the longest lists.
Hills’s program further revealed that the most successful students abandoned one category of animals for another when it took too long to name a new animal, just as a foraging animal leaves behind a patch of food when its time would be better spent at a more fruitful patch. The findings appear online in the February 13 issue of Psychological Review.
While the study addresses only a particular kind of memory, or remembering activity, the significance of the investigation may not lie only in the questions it answers about memory function. The results support the more general investigation of whether higher level cognitive abilities evolve from more fundamental ones, like spatial foraging mechanisms. According to Hills,
Before we had abstract thinking, we had brains that helped us get around physical spaces—some of those abilities may be co-opted to search in information space.
Foraging mechanisms have already been used to explore how we search for information, on the web for example.
But in October, I discussed a related idea described in an article on vision at Physicsworld.com. The piece contrasted the fractal pattern of the searching eye with the restrictive stillness of digital imaging technology.
Richard Taylor and his colleagues at the University of Oregon investigated this movement or how we search for information in a complex scene. By tracking the motion of the eye they found that the eye searches one area with short steps before jumping a larger distance to another area, which it again searches with small steps, and so on, gradually covering a large area.
And there is the work done to investigate how the body represents spatial information in the activity of what neuroscientists call grid cells in the brain:
Grid cells provide geometric coordinates for locations and help the brain generate an internal grid to help in navigation. Along with place cells, which code for specific locations, head direction cells, which act like a compass, and border cells, which define the borders of an environment, grid cells enable to brain to generate a series of maps of different scales and help with recognition of specific landmarks.
One of the keys to how these things may be related to mathematics lies in the observation of planned action, studied by cognitive scientists and cited by Yehuda Rav (in his essay on Mathematics and Evolutionary Epistemology)
When we form a representation for possible action, the nervous system apparently treats this representation as if it were a sensory input, hence processes it by the same logico-operational schemes as when dealing with an environmental situation.
I have little doubt that mathematics emerges from all that the body knows and all of the ways that it can act. Looking at how the nervous system interacts with conceptual or internally generated worlds can tell us quite a lot, not only about the content of mathematics, but also about how it is motivated and, perhaps, what it means to be human.
By Joselle, on April 10th, 2012 If one is paying attention, questions about the relationship between mathematics and reality just get more interesting. Mathematician Alain Connes is certainly the modern representation of the Platonic view that mathematical reality is a discoverable, fully existent reality. But there is also the view from MIT cosmologist Max Tegmark that our physical world is not only effectively described by mathematics but, rather, that it is a mathematical structure. And then there is the perspective of some quantum information theorists, like Vlatko Vedral, that information (defined largely by the concept of probability) is what builds the fabric of the universe. He presents this thesis in his book Decoding Reality which has recently come out in paperback. Vedral spoke about the book in an interview for The Guardian two years ago.
These ideas shift the context within which one would consider the Lakoff/Nunez view of mathematics – that it is an elaboration (through conceptual metaphor) of more fundamental experiences of the body. Mathematics, in this sense, is a purely human, body-driven cognitive tool. One of the difficulties I have had with this idea is that, while it connects mathematics to cognitive systems within us, it neglects what I think is important, namely that cognitive action can only be fully understood within the unity of a body-and-its-world. Inevitably, what we come to think about the nature of our physical reality will impact how we understand cognition as well as mathematics.
The complexity of these questions is highlighted again by articles like Bits of Reality by Tom Siegfried in Science News on April 7. Siegfried puts the birth of Vedral’s quantum information theory in place:
Quantum mechanics arose in the 1920s as the math for describing the odd behavior of atoms and electrons; information theory came along two decades later, as formulas for quantifying communication over telephone lines. For decades the two theories led separate lives in fields of study far removed from one another. While physicists expended their intellectual energy on uniting quantum mechanics with relativity (a quest that continues, still without success), information scientists graduated from telephones to computers with only occasional concern for quanta. But then in the 1980s and ’90s, quantum and information science met, married and produced offspring — specifically, the intellectual enterprise known today as quantum information theory.
Initially, quantum information snared the attention of physics fans for its possible uses in sending secret codes and creating superfast computers…But theorists pursuing quantum information’s secrets are more motivated by the quest to acquire a deeper understanding of physical reality, and perhaps to grasp more fully the nature of quantum mechanics itself.
Even in their abstraction, the contrast between the bit of computer information and the qubit of quantum information theory is interesting. Both rely on the on/off, yes/no, of the computer world’s 1’s and 0’s.
But a qubit is infused with quantum magic, allowing it be both a 1 and a 0 at the same time. This “superposition” of identities gives quantum information extraordinary power.
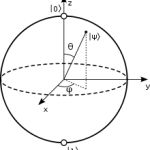
The possible states of a qubit are visualized with a sphere, the one known as a Bloch sphere. A classical bit could only be found at either the north or south pole of the sphere. But a pure qubit state could be represented by any point on its surface.
What I find interesting in this story is the relaying that seems to be happening between math and physics. Quantum mechanics is, first, the mathematics used to describe the behavior of atoms and electrons, and information theory is comprised of the formulas used to describe communication lines. But the mathematics of quantum mechanics now informs quantum information theory. And, in 1994, mathematician Peter Shor proved that a quantum computing algorithm could solve the very difficult problem of finding the prime factors of a number hundreds of digits long. According to physicist John Preskill,
Factoring is a hard problem classically, but Shor’s algorithm shows that it is an easy problem quantumly. And so it seems the boundary between what problems are hard and what problems are easy is different in our physical world — because it’s a quantum world — than it would be if the world were classical.
Siegfried notes:
Quantum information could reveal nuances about the interface between mathematics and the physical world.
And he goes on to discuss the role quantum information theory plays in efforts to identify the physical principles from which the strange rules of quantum mechanics emerge.
…in recent decades, the quest to find a physical principle from which quantum mechanics can be built has become more popular, and quantum information has been at the heart of many such efforts. Much of the work along these lines was inspired by the late physicist John Archibald Wheeler, who believed that quantum physics — and existence itself — might have its roots in aspects of information theory. His slogan “it from bit” summarized the view that reality somehow emerges from cosmic information processing.
Vlatko Vedral is one of the people who picked up that ball. Vedral defends his optimism (in a recent blog for the Huffington Post) that even if quantum physics is replaced by a new theory, only some of the arguments in his book will need revising. And there he makes the following remark:
Likewise, I argued that living systems might be using quantum physics to process information more efficiently. This too fails in the post-quantum world, which again is likely to be good news, but it might also bring a new twist on the relationship between physics and biology. Could it be, as one of the pioneers of quantum physics Erwin Schroedinger alluded a long time ago, that biology will force us to come up with new laws of physics?
-certainly.
By Joselle, on April 2nd, 2012 Alain Connes is currently a professor at the College de France and Vanderbilt University. Connes won the Fields Medal in 1982 and Crafoord Prize in 2001. He has authored a number of books and represented the Platonist point of view in a debate with neuroscientist Jean-Pierre Changeux presented in the Princeton book: Mind, Matter and Mathematics.
Connes is one of the few mathematicians who can speak about his experience of mathematics in an intimate and provocative way. He’s like the guide you were fortunate to get, when you made your trip to an old city, who made your trip memorable because he directed your attention to the things most likely to tell you where you were and what you were looking at. What follows are a few excerpts from some of his writing. I don’t have much to add to what he writes, other than saying that his view contributes significantly to my own, and to the ongoing debate about what mathematics is. The first set of excerpts is from a paper called A View of Mathematics.
The nature and inner workings of this mental activity are often misunderstood or simply ignored even among scientists of other disciplines. They usually only make use of rudimentary mathematical tools that were already known in the XIXth century and miss completely the strength and depth of the constant evolution of our mathematical concepts and tools.
It might be tempting at first to view mathematics as the union of separate parts such as Geometry, Algebra, Analysis, Number theory etc…where the first is dominated by the understanding of the concept of “space,” the second by the art of manipulating “symbols,” the next by the access to “infinity” and the “continuum” etc…it is virtually impossible to isolate any of the above parts from the others without depriving them from their essence. In that way the corpus of mathematics does resemble a biological entity which can only survive as a whole and would perish if separated into disjoint pieces.
Whereas the letters we use to encode numbers are dependent of the sociological and historical accidents that are behind the evolution of any language, the mathematical concept of number and even the specificity of a particular number such as 17 are totally independent of these accidents.
The scientific life of mathematicians can be pictured as a trip inside the geography of the “mathematical reality” which they unveil gradually in their own private mental frame…whatever the origin of one’s itinerary, one day or another if one walks long enough, one is bound to reach a well known town i.e. for instance to meet elliptic functions, modular forms, zeta functions. “All roads lead to Rome” and the mathematical world is “connected”. In other words there is just “one” mathematical world, whose exploration is the task of all mathematicians and they are all in the same boat somehow.
Moreover exactly as the existence of the external material reality seems undeniable but is in fact only justified by the coherence and consensus of our perceptions, the existence of the mathematical reality stems from its coherence and from the consensus of the findings of mathematicians. The fact that proofs are a necessary ingredient of a mathematical theory implies a much more reliable form of “consensus” than in many other intellectual or scientific disciplines. It has so far been strong enough to avoid the formation of large gatherings of researchers around some “religious like” scientific dogma imposed with sociological imperialism.
Most mathematicians adopt a pragmatic attitude and see themselves as the explorers of this “mathematical world” whose existence they don’t have any wish to question, and whose structure they uncover by a mixture of intuition, not so foreign from “poetical desire,” and of a great deal of rationality requiring intense periods of concentration. Each generation builds a “mental picture” of their own understanding of this world and constructs more and more penetrating mental tools to explore previously hidden aspects of that reality.
On the concept of space:
The mental pictures of geometry are easy to create by exploiting the visual areas of the brain. It would be naive however to believe that the concept of “space” i.e. the stage where the geometrical shapes develop, is a straightforward one. In fact as we shall see below this concept of “space” is still undergoing a drastic evolution.
The Cartesian frame allows one to encode a point of the Euclidean plane or space by two (or three) real numbers… This irruption of “numbers” in geometry appears at first as an act of violence undergone by geometry thought of as a synthetic mental construct.
This “act of violence” inaugurates the duality between geometry and algebra, between the eye of the geometor and the computations of the algebraists, which run in time contrasting with the immediate perception of the visual intuition.
Far from being a sterile opposition this duality becomes extremely fecund when geometry and algebra become allies to explore unknown lands as in the new algebraic geometry of the second half of the twentieth century or as in noncommutative geometry, two existing frontiers for the notion of space.
Some of these remarks are restated in a short paper called Advice to the Beginner, along with a number of other interesting observations. This paper can be accessed from his publications list.
From an Interview for the European Mathematical Society:
For me, algebra unfolds in time: I can see a formula live and turn and exist in time, whereas geometry has something instantaneous about it and I have much more difficulty with it. As far as I go, formulas create mental pictures.
I have often had the impression that there are concentric circles in the mathematical world ; that one begins to work in a totally eccentric part and one tries to get gradually closer to the heart.
What is this heart ? Is it subjective ?
What I mean by the heart of mathematics is that part which is interconnected to essentially all others. A bit like all roads lead to Rome, what I mean is that, when the mental picture you get of a mathematical subject becomes more and more precise, you realize in fact that, whatever the topic you begin with, if you look at it sufficiently precisely, after a while, it converges toward this heart…. if you walk long enough, you are obliged to go towards these domains, you cannot remain outside. If you do, it is a bit out of fear. You can succeed in doing a lot of things by refining techniques in a given topic, but unless you keep moving towards this heart you feel you are left outside.
Perhaps one of the things that discourages so many:
There is always this permanent fear of error which doesn’t improve over the years… And there is this part of the brain which is permanently checking, and emitting warning signals.
By Joselle, on March 26th, 2012 I’ve always been intrigued by the sensation of movement in music. And it is fair to say that it was my first calculus class that led me to graduate study in mathematics because, for the first time, I saw movement in mathematics. My fascination with each of these was nudged again by an interview with jazz pianist Vijay Iyer that I heard on NPR’s All Things Considered.
Once a graduate student of math and physics at Yale, Iyer’s attention eventually turned to music and the study of music perception and cognition. It was improvisation on the piano (unlike the lack of improvisation in his training on the violin) that brought Iyer to consider that it is the relationship between the body’s movement and an abstract idea that together make music.
One thing that has kind of obsessed me at the piano for maybe the last decade or so is just listening to what my hands would do with the instrument. So the keys’ action speak… It all lays right under the hands… It comes from the physical logic of the hand at the keyboard. To me, they’re gestures. You know, they’re physical gestures. I hear the sweep of a hand in those shapes…- it’s this physical thing that’s also something that resorts to a logic that’s very nonphysical. Letting these numbers unfold through physical action is, for me, part of the process of making music.
Iyer brings it all round to some very primal things.
Particularly, what music is for us as people is it’s a sound of other people. For example, the way we perceive rhythm is by imagining ourselves moving. So there is a really primal connection between music and the body.
…it’s about the rhythms that are inherent to the body. Breathing is one of those. Heartbeat is another. Speech is another. And those are all timescales that correspond to musical activity.
It’s probably easier for us to appreciate music as an action, than say mathematics as an action. But they each rely on movement.
Out of the early twentieth century debate between the formalists and the intuitionists sprang this claim from L.E. J. Brouwer that mathematics has its origin in the movement of time. Expressed as the First Act of Intuitionism it calls for:
Completely separating mathematics from mathematical language and hence from the phenomena of language described by theoretical logic, recognizing that intuitionistic mathematics is an essentially languageless activity of the mind having its origin in the perception of a move of time. This perception of a move of time may be described as the falling apart of a life moment into two distinct things, one of which gives way to the other, but is retained by memory. If the twoity thus born is divested of all quality, it passes into the empty form of the common substratum of all twoities. And it is this common substratum, this empty form, which is the basic intuition of mathematics.
Brouwer’s extreme intuitionism challenged the legitimacy of far too many mathematical constructions, to be realistically accepted by the mathematics community. But no doubt there is a strong link between our conceptual worlds and our experiences of space and time.
The manifold expressions of mathematical movement are beautifully described in some of Fritjof Capra’s The Science of Leonardo.
The book contains wonderful descriptions of the paths taken by Leonardo’s thoughts, and how they line up with modern developments in mathematics as well as the growing insights into cognition itself. But perhaps these passages are most relevant at the moment:
In contrast to Euclid’s geometry of rigid static figures, Leonardo’s conception of geometric relationships is inherently dynamic. This is evident even from his definitions of the basic geometric elements. “The line is made with the movement of the point,” he declares, “The surface is made by the transverse movement of the line;…the body is made by the movement of the extension of the surface.”
Leonardo also drew analogies between a segment of a line and a duration of time: “The line is similar to a length of time, and as the points are the beginning and end of the line, so the instants are the endpoints of any given extension of time.” Two centuries later this analogy became the foundation of the concept of time as a coordinate in Descartes’ analytic geometry and in Newton’s calculus.
As mathematician Matilde Macagno points out, on the one hand Leonardo uses geometry to study trajectories and various kinds of complex motions in natural phenomena; on the other hand, he uses motion as a tool to demonstrate geometrical theorems. He called his approach “geometry which is demonstrated with motion.”
It’s as if he could place himself completely within what he saw instead of outside of it.
One of the things I found most interesting was that, in the absence of mathematics that could describe dynamic systems, Leonardo made scientific drawings (shown in the book). These are beautiful drawings, rich with observation. Capra explains that these were not realistic representations of a single view.
Rather they are syntheses of repeated observations, crafted in the form of theoretical models.
I particularly like this description of Leonardo’s mathematics:
Since Leonardo’s science was a science of qualities, or organic forms and their movements and transformations, the mathematical “necessity” he saw in nature was not one expressed in quantities and numerical relationships, but one of geometric shapes continually transforming themselves according to rigorous laws and principles. “Mathematical” for Leonardo referred above all to the logic, rigor, and coherence according to which nature has shaped, and is continually reshaping, her organic forms.
And this one of his science:
Leonardo’s studies of the living forms of nature began with their outward appearance and then turned to methodical investigations of their intrinsic nature. Life’s patterns of organization, its organic structures, and its fundamental processes of metabolism and growth are the unifying conceptual threads that interlink his knowledge of macrocosm and microcosm.
Capra also makes the argument that da Vinci’s concept of the soul bears a strong resemblance to contemporary ideas that identify the mind, or cognition with the process of life. What Leonardo’s soul shares with current ideas about cognition is their two-fold nature. Today, cognition (like Leonardo’s soul) is both the process of perception and the process that animates the movement and organization of the body. Leonardo often wrote about it in terms of action. And in this light, Capra refers to his notes on the flight of birds.
Over many hours of intense observations of birds of flight in the hills surrounding Florence, Leonardo became thoroughly familiar with their instinctive capacity to maneuver in the wind, keeping their equilibrium by responding to changing air currents with subtle movements of their wings and tails. In his notes he explained that this capacity was a sign of the bird’s intelligence – a reflection of the action of its soul.
By Joselle, on March 19th, 2012 If you’ve been reading my posts, you’ve probably figured out that this blog is motivated, to a large extent, by my fascination with what mathematics can help us see about the source, targets and bewildering range of human cognition. My expectations rest on the idea that what we have come to call the human mind is necessarily grounded in those same elements whose infinite combinations produce the entire fabric of the natural world. This is not to say that the human experience of transcendence is an illusion, but rather that we have yet to grasp the full expanse of nature.
A few things that I read today point to this idea from different directions. While the topics may seem unrelated, they are each pieces of a puzzle on which I’m always working. The first, a Scientific American report, caught my attention with its title: Worm Discovery Illuminates How Our Brains Might Have Evolved. The study looked at a particular worm, the acorn worm.
These unlovely, simple little worms live most of their brainless lives buried in deep-sea beds. Researchers have probed the genetic patterns of their developing larvae and think they might have discovered a set of signals similar to the ones we use to build our central nervous system. The findings are reported online in the same issue of Nature.
“The vertebrate brain is really exquisitely complex and elaborate,” says Ariel Pani, a graduate researcher at Stanford University and co-author of the new paper. The brain is prompted into being during development by a long chain of genetically determined signals. “There are particular developmental processes in vertebrates that seem to be absent in other species”—or at least those that have been most commonly studied, such as the amphioxus, Pani notes. Thus, many scientists had presumed that these genetic tools had only emerged with the vertebrate line itself.
But the new findings challenge this idea if genetic cues in embryonic worms resemble those responsible for setting off the major divisions of the central nervous system in vertebrates. In the worm, these genetic signals direct the development of the animal’s ectoderm, which contains sensory cells.
That would mean that the vertebrate brain “didn’t invent entirely new mechanisms—it took existing ones to develop a completely new structure,” Pani explains. If the genome is the proverbial set of blueprints for an organism, the signaling centers involved in embryonic development are like the early pieces of the scaffolds. “Vertebrates have that same sort of framework and are turning it into a very fancy Frank Lloyd Wright house, and hemichordates have turned it into a little cottage.”
But many in the research community are not convinced.
The researchers have found gene interactions that are involved in body patterning dividing their heads from their tails—and not much more, says Linda Holland, a research biologist at Scripps Institution of Oceanography who was not involved in the new research. “It’s not uncommon for an animal to have part of a gene network” without possessing the entire workup, she notes.
This report pointed me to a September 2009 special issue of Scientific American devoted to origins. It contained an article by Marc Hauser (professor of evolutionary biology a Harvard) concerned with the origin of the human mind. Hauser is concerned less with the building blocks and more with what distinguishes human cognition:
Researchers have found some of the building blocks of human cognition in other species. But these building blocks make up only the cement footprint of the skyscraper that is the human mind. The evolutionary origins of our cognitive abilities thus remain rather hazy.
But these building blocks are not ones like the signaling found in the worm. They are more the communication skills or the number sense we share with other creatures.
I think that one of the more important insights into human cognition described here is what Hauser calls promiscuous interfaces – the ability to make promiscuous connections between systems of understanding anchored in different brain regions. As an example, he describes the effect of recursive operations (a powerful fuel for many imagined things including mathematical ideas).
All creatures are endowed with recursive motor machinery as part of their standard operating equipment. To walk, they put one foot in front of the other, over and over again. To eat, they may grasp an object and bring it to the mouth repeatedly until the stomach sends the signal to stop. In animal minds, this recursive system is locked away in the motor regions of the brain, closed off to other brain areas. Its existence suggests that a critical step in acquiring our own distinctive brand of thinking was not the evolution of recursion as a novel form of computation but the release of recursion from its motor prison to other domains of thought.
Promiscuous interfaces are the living tissues on the bones of mathematics.
Finally, in a February posting on the blog Bering in Mind Jesse Bering writes on autistic savants. Here, I was most intrigued by the talents of autistic calendar calculators – individuals who could correctly identify the day of the week for any date you might give them.
After conducting a series of experiments meant to probe the techniques of perhaps the fastest living autistic-savant calendar calculator (a 21-year-old man named “Donny” with an IQ of 71 who tested at a 98 percent level accuracy in naming the weekday of any date between the year 1 and the year 9999, at speeds up to 700 ms), Marc Thioux and his colleagues from the Yale School of Medicine conclude that the starting point for such an awe-inspiring capacity is the autistic child’s preoccupation with numbers and dates, in combination with a penchant for repetition and ritual.
Bering explains that:
…a mathematician, on the other hand, might explain the formulae of perpetual calendars, such as the 28-year rule (the same calendars are shared by two years 28 years apart within the same century) and Pope Gregory’s exception to this rule, in which he declared in 1582 that century years are not leap years unless they’re divisible by 400.
Researchers argue that
…calendar calculation in autistic savants involves a mix of rote memory for previous dates and, eventually (at least for some, like Donny), an implicit understanding of the underlying algorithms driving the Gregorian calendar, such as the fact that if a non-leap year starts on a Sunday, the following year will begin on a Monday. (emphasis my own)
The worm, promiscuous connections, and calendar calculators are not topics that flow easily from one to the other, but they each trigger important questions about how, for example, thought is physical, or how the body creates its complex intellectual world, or what it means to have an implicit understanding of an underlying algorithm. There is wonder in the fact that the nervous system, as David Deutsch once remarked, has developed into a physical system that can build, with increasing precision, models of the whole of our physical reality. I’m convinced that the evolution of mathematical ideas can tell us something about the evolution of cognition.
By Joselle, on March 12th, 2012 I was still a graduate student when I first imagined that mathematics was actually outlining our cognitive potential (what we could see and understand). I considered writing a paper called An Asymptotic Approach to a Theory of All the Things, convinced that as the mind grew it would continue to approach the reality behind perception, but never quite get there. I never wrote the paper. But a special issue of Nature, that is a tribute to Alan Turing, brought it to mind.
It is Turing’s foresight into embodiment ideas and the way he was able to tread the shared boundaries of mathematics and biology that triggered my memory.
In one of the pieces, The incomputable reality, Barry Cooper (The School of Mathematics, University of Leeds, UK) makes the case that Turing’s work can build new bridges between mathematics and physics.
Turing was interested in the mathematics of computing and also in its embodiment – the material environment that houses it. This theme links all of his work from machines to the brain to morphogenesis. Although many mathematicians and software engineers today see it as irrelevant, embodiment is key to explaining the physical world.
Cooper likens the Universe to a turbulent stream:
A river swollen by recent rain occasionally erupts into surprising formations that we would not expect from the basic dynamics of water flow. The reason is coherence – non-local connectivity affects the water’s motion. Turbulence and other ‘emergent’ nonlinear phenomena, may not be computable with a Turing machine. Zebra stripes and tropical fish patterns, which Turing described in 1952-54 with his differential equations for morphogenesis, arise similarly.
…Modeling the evolution of the higher order effects is difficult in anything other than a broad-brush way.
Cooper argues that, like the stream, the behavior of the Universe “has many emergent levels of causality, bridged by phase transitions…We are part of an organic whole – fragmented but coherent.” He calls for a “renewed respect for embodied computing – as anticipated in Turing’s late work in the 1950’s…”
Answering the claim that Turing computation does not create anything that is not there already in the initial data, Cooper suggests
If we look at the world with new eyes, allowing computation full expression, we may come to startling conclusions.
Another piece in this special issue, Pattern formation, is from John Reinitz (University of Chicago). His piece focuses on mathematics and also references Turing’s 1952 paper.
Alan Turing’s 1952 paper on the origin of biological patterning solved an intellectual problem that had seemed so hopeless that it caused a great developmental biologist, Hans Driesch, to give up science and turn to the philosophy of vitalism.
Reinitz is speaking about the nineteenth century recognition that animal bodies develop from a pattern-less single cell, and not from a microscopic “preformed version of the adult body.” The self-organizing activity of cells could not be understood with the ideas of that century.
Before the invention of computers, applied mathematics dealt only with linear differential equations, which can amplify a pattern but not generate it.
And this is the fun part, where Turing builds some bridges – from linearity to pattern, from math to biology, from century to century. He accomplishes this by finding a way to manage diffusion (or the spontaneous intermingling of substances) before there is a way to fully represent it.
Turing’s argument involved a mathematical trick: he created a nonlinear system by turning on diffusion discontinuously in an otherwise linear system at a specific instant. Without diffusion the system is stable and homogeneous, but with diffusion, it becomes unstable and forms spatial pattern. The brilliance of the trick is that the nonlinearity is confined to a single point in time, so that at all other times, only the theory of linear equations is needed. Turing cleverly arranged to have diffusion generate pattern, rather than blur it, as it usually does.
Turing used analytic arguments of the nineteenth century to point the way towards the computational science of the twenty-first century.
This is a fine example of using what can be seen without being misled by it. Turing illuminated the path to an insight with mathematics.
|
|



Recent Comments