Roger Antonsen came to my attention with a TED talk recorded in 2015 that was posted in November. Characterized by the statement, “Math is the hidden secret to understanding the world,” it piqued my curiosity. Antonsen is an associate professor in the Department of Informatics at the University of Oslo. Informatics has been defined as the science of information and computer information systems but its broad reach appears to be related to the proliferation of ideas in computer science, physics, and biology that spring from information-based theories. The American Medical Informatics Association (AMIA) describes the science of informatics as:
…inherently interdisciplinary, drawing on (and contributing to) a large number of other component fields, including computer science, decision science, information science, management science, cognitive science, and organizational theory.
Antonsen describes himself as a logician, mathematician, and computer scientist, with research interests in proof theory, complexity theory, automata, combinatorics and the philosophy of mathematics. His talk, however, was focused on how mathematics reflects the essence of understanding, where mathematics is defined as the science of patterns, and the essence of understanding is defined as the ability to change one’s perspective. In this context, pattern is taken to be connected structure or observed regularity. But Antonsen highlights the important fact that mathematics assigns a language to these patterns. In mathematics, patterns are captured in a symbolic language and equivalences show us the relationship between two points of view. Equalities, Antonsen explains, show us ‘different perspectives’ on the same thing.
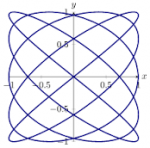
In his exploration of the many ways to represent concepts, Antonsen’s talk brought questions to mind that I think are important and intriguing. For example. what is our relationship to these patterns, some of which are ubiquitous? How is it that mathematics finds them? What causes them to emerge in the purely abstract, introspective world of the mathematician? Using numbers, graphics, codes, and animated computer graphics, he demonstrated, for example, the many representations of 4/3. And after one of those demonstrations, he received unexpected applause. The animation showed two circles with equal radii, and a point rotating clockwise on each of the circles but at different rates – one moved exactly 4/3 times as fast as the other. The circles lined up along a diagonal. The rotating point on each circumference was then connected to a line whose endpoint was another dot. The movement of this third dot looked like it was just dancing around until we were shown that it was tracing a pleasing pattern. The audience was clearly pleased with this visual surprise. (FYI, this particular demonstration happens about eight and a half minutes in) Antonsen didn’t expect the applause, and added quickly that what he had shown was not new, that it was known. He explains in his footnotes:
This is called a Lissajous curve and can be created in many different ways, for example with a harmonograph.
These curves emerge from periodicity, like the curves for sine and cosine functions and their related unit circle expressions. In fact it is the difference in the periods described by the rotation of the point around each of Antonsen’s circles (a period being one full rotation) that produced the curve that so pleased his audience.
I believe that Antonsen wanted to make the point that because mathematics brings a language to all of the patterns that emerge from sensation, and because it is driven by the directive that there is always value in finding new points of view, mathematics is a kind of beacon for understanding, everything. About this I wholeheartedly agree. I have always found comfort in the hopefulness associated with finding another point of view, and the powerful presence of this drive in mathematics may be the root of what captivates me about it. Mathematics makes very clear that there is no limit to the possibilities for creative and careful thought.
But I also think that the way Antonsen’s audience enjoyed a very mathematical thing deserves some comment. They didn’t see the mathematics, but they saw one of the things that the mathematics is about – a shape, a pattern, that emerges from relationship. And their impulse was to applaud. This tells us something about what we are not accomplishing in most of our math classes.


Recent Comments