|
|
By Joselle, on January 10th, 2011 Last week I pointed to a few discussions of mathematics I found interesting and this is my first chance to follow up. One of them took note of the surprising persistence of a platonic view of mathematical objects, a view that inevitably introduces into our scientific culture some version of a metaphysical idea. Paul Bernays addresses it directly in a 1935 essay. He draws attention to the difference between the way Euclid describes a line and the way Hilbert did.
we notice that Euclid speaks of figures to be constructed whereas, for Hilbert, system of points, straight lines, and planes exist from the outset. Euclid postulates: One can join two points by a straight line; Hilbert states the axiom: Given any two points, there exists a straight line on which both
are situated. “Exists” refers here to existence in the system of straight lines.
This example shows already that the tendency of which we are speaking consists in viewing the objects as cut off from all links with the reflecting subject.
From the point of view of mathematics using totalities, of numbers, of functions, of sequences (in other words, all of a particular class of objects) Bernays makes clear,
constructive definitions of special functions, sequences, and sets are only ways to pick out an object which exists independently of, and prior to, the construction.
Bernays gives a number of examples in which the existence of a class of objects is accepted before a particular one is constructed. Hence he says easily, “it is not exaggeration to say that Platonism reigns today in mathematics.” But he also indicates that the paradoxes which arose from the discussion of totalities, removed the possibility that there is some other world where these objects exist, and requires that we consider only a restricted Platonism – “an ideal projection of a domain of thought.”
A well-known contemporary debate between the neurobiologist Jean-Pierre Changeux and the prominent mathematician Alain Connes is presented in the book Conversations on Mind, Matter, and Mathematics. Here Connes defends the truly Platonic perspective and makes the following point:
Projective representations of mathematical objects are certainly physical brain states, but reducing mathematical reality to these states would be like reducing literature to the chemical reactions of ink and paper.
An interesting review of the book by Michael Atiyah can be found here.
Raphael Nunez, the cognitive scientist, would agree but for very different reasons. For him, mathematics develops by virtue of inference-preserving conceptual metaphors. In other words something in our experience is mapped to an abstract idea in such a way that the abstract idea preserves the implications of the original experience. (See – Numbers and Arithmetic: Neither Hardwired Nor Out There).
But the body is built to find generalities, create ideals. It’s part of how the tissue of which we’re made responds to the world. This is described in an earlier post: Zeki, The Brain and the Art of Abstraction.
It seems to me that what mathematics may be providing is an opportunity to correct our usual perspective. An unwillingness to accept a truly platonic view of the world is partly due to our materialistic tendencies, but also to our habit to distinguish ourselves from all that we are part of. By this I mean that Changeux’s and Nunez’s views make sense because we accept the idea that human thoughts are only human or purely human. I do not find this self-evident at all. Human imagination grows out of the world and so must be related to it in some way. It seems that mathematics is powerful by virtue of the fact that it moves easily, back and forth, between its role as a language for science (or for the material) and the way it relies on non-material ideals. In other words, it is comfortable with what the senses perceive and what they don’t. It’s neurobiological source shows its relation to life at the cellular level. Its role in revealing the inaccessible properties of quantum mechanical worlds reveals the reach of implications it may have inherited from our more common experiences. Side by side, these things challenge the boundary between what is human and everything we believe is not, even between what is conscious and everything we believe is not. This is why, when mathematics is the subject of the discussion, a platonic view of things persists.
By Joselle, on January 6th, 2011 Many of this week’s circumstances are limiting the time I have to write but I would like to point to a few sources that contain very nice accounts of what is known as the foundational crisis in mathematics. One of them was written by Paul Bernays in 1935. Understanding the nature of some of the 19th and 20th century disputes among mathematicians reveals quite a lot about the character of mathematical objects and what motivates their exploration – things that could easily slip by even the conscientious math student.
The discussions that kept me reading were those centered around the following:
*understanding how there was once a debate among mathematicians about whether mathematical objects should ultimately be understood conceptually or computationally.
*a persistent Platonism or how, or to what extent, a mathematical object can be detached from the thinking subject
*what is it that makes modern mathematics modern
I would like to devote a post to each of these topics. Because of the limitations on my time today, I will only provide some links.
Jose Ferreiros’ essay The Crisis in the Foundations of Mathematics appears in Princeton’s Companion to Mathematics edited by Timothy Gowers. A pdf version is available here. In it he says:
The foundational debate has also contributed in a definitive way to clarifying the peculiar style and methodology of modern mathematics, especially the so-called “Platonism” or “existential character” of modern mathematics…
And he then refers to Bernays’ 1935 paper. In this paper, Bernays talks about
a restricted Platonism which does not claim to be more than, so to speak, an ideal projection of a domain of thought.
By this he means that the ideal resides in and is the product of thought rather than living in some other ideal world. But it is an ideal none-the-less and will not changed by the thoughts of an individual contemplating it.
Both the Ferreiros essay and a review of a book by Ferreiros (The Architecture of Modern Mathematics) from Andrew Arana talk about Riemann’s preference for conceptually defined mathematical objects over computationally defined ones. Arana says clearly about the 19th century struggle with how best to think about complex numbers,
This was (roughly) a struggle between two camps, one led by Riemann, the other led by Weierstrass. Weierstrass and his followers thought complex analysis should be `arithmetized’, meaning in particular that analytic functions should be defined as functions representable by power series. By contrast, Riemann and his followers favored representation-independent definitions, which in practice meant defining analytic functions as those satisfying the Cauchy-Riemann equations. The Riemannian approach then develops the theory of analytic functions without having to consider particular explicitly defined analytic functions. Riemann pioneered the term “geometric” for this kind of approach to analysis, but this wasn’t a stretch: he encouraged visualization in analysis, developing the notion of a Riemann surface to help.
Ferreiros’ essay makes the point that the defining characteristics of the modern methods of the 19th and 20th centuries are the following:
the notion of an ‘arbitrary’ function (proposed by Dirichlet), i.e. one whose relation is not written explicitly.
infinite sets and a higher infinite
conceptual definitions with an emphasis on structure
a reliance on purely existential methods of proof
It would be interesting to consider the intellectual shifts in modern mathematics alongside what has been said about the intellectual shifts in modern art. I will do some thinking about this.
By Joselle, on December 29th, 2010 I don’t have a lot of time to write this week and next but I felt a little surge of thoughts gather when I read about the implications of Einstein’s Second Law (m = E/c^2) which is a simple rearrangement of the now famous E = mc^2. It was in The Lightness of Being by Frank Wilczek. Here’s what Wilczek says:
Einstein’s first law is of course E = mc^2. Famously the first law suggests the possibility of getting large amounts of energy from small amounts of mass. It calls to mind nuclear reactors and nuclear bombs.
Einstein’s second law suggests something quite different. It suggests the possibility of explaining how mass arises from energy.
This was the thought Einstein pursued.
Wilczek preceded his discussion of Einstein’s concept of energy with an anecdote about Paul Dirac – specifically, that when asked how he discovered new laws of nature, he responded, “I play with equations.”
Although the same equation written different ways may be algebraically or logically equivalent, their different arrangements can suggest very different things. It was around this point that my own thoughts began to gather, in an almost reflexive way.
To begin with, it’s interesting that two symbolic representations of relationship, each of which can be said to contain exactly the same information, can narrate different stories, or create different images. In this case, one arrangement of the equation tells the story of getting energy out of matter and the other about the origins of mass. This says something about how we, human beings, work – about how we can turn something upside down and actually find something else. It also says something about what mathematics accomplishes, how it captures insurmountable mysteries and re-presents them on paper, where doodles sometimes live, and where they can then be toyed with, investigated, and used as probes. Ideas about how the universe works do emerge from relationships among numbers.
As bewildering, complex and dense as it may seem, mathematics is everywhere about relationship. It is an unbounded exploration of how things can be related, numbers, lines, spaces, fields…or, even more to the point, it is the investigation of all of the possibilities for relationship. This is exactly why its generalities are stripped of every particular and why the few symbols of an equation can do so much.
How mass arises is a question physicists have yet to answer. I referred to their search for the elusive Higgs particle (the expected answer to that question) in an earlier post. This recent article in Nature expresses the determination of experimentalists at the Large Hadron Collider in Geneva Switzerland to find it if it is there to be found.
By Joselle, on December 20th, 2010 Let’s ask again, “What is the nature of the bridge between sense perceptions and concepts? It’s a simple question to ask, but a fairly difficult one to answer.
Raphael Nunez contributed a chapter to the Springer book, Recasting Reality: Wolfgang Pauli’s Philosophical Ideas and Contemporary Science. A pdf of the chapter can be found here. In it he surveys some of Pauli’s ideas as he takes note of the work of both Kepler and Jung. Nunez then looks at how his own work, a cognitive idea analysis of mathematics, relates. Here are a few of the references I most enjoyed. Nunez quotes from a 1952 essay of Pauli’s:
The process of understanding nature as well as the happiness that man feels in understanding, that is, in the conscious realization of new knowledge, seems thus to be based on a correspondence, a `matching’ of inner images pre-existent in the human psyche with external objects and their behavior. This interpretation of scientific knowledge, of course, goes back to Plato,and is, as we shall see, very clearly advocated by Kepler.
And Pauli explains Kepler’s understanding:
He [Kepler] speaks in fact of ideas that are pre-existent in the mind of God and were implanted in the soul, the image of God, at the time of creation. These primary images which the soul can perceive with the aid of an innate`instinct’ are called by Kepler archetypal (`archetypalis’). Their agreement with their ‘primordial images’ or archetypes introduced into modern psychology by C.G. Jung and functioning as `instincts of imagination’ is very extensive.”
Then Jung in a letter to Pauli in 1953, talking about whole numbers, explains that they:
possess that characteristic of the psychoid archetype in classical form – namely, that they are as much inside as outside. Thus, one can never make out whether they have been devised or discovered; as numbers they are inside and as quantity they are outside.”
In the end Nunez outlines, in some detail, how research in cognitive science shows us that sense perceptions and concepts (particulary mathematical ones) are bridged by image schemas, and that human conceptual systems can be decomposed into primitive concepts of spacial relations – like something being “above” something else or “in contact with” something else or “supporting” something else.
What I find most intriguing is that even though the language about it may change, and so may the method of investigating it, the wonderment about things, which are not being constructed from sensory data, persists. Inevitably we are led to consider that there is some aspect to reality that transcends the physical and the temporal. Many modern thinkers have rejected the notion that there is anything more than the physical. But I think that’s missing the point. And the so-called Platonic view of mathematics keeps the question alive. Mathematics is still permitted some mystery. I think it points, as Jung observes, both inside and out and, as Plato once thought, has the unique ability to bridge the real world and the world of images.
In what way is the whole of reality expressed in us? What are we doing when we find representations of things which are not immediately before us or perceived by the senses? How are we related to all there is?
Cognitive science does provide a new window, another view of things, when it looks at what the body does, at the integration of the processes of attention, perception and memory, or the neural dynamics of these processes as well as physiological processes outside of our awareness. It looks to me like ordering is the key, that by ordering the senses build the world. But language and symbol also order. And what they build is there, in much the same way as a tree is there. Everything we live in, physically and culturally, is there. Merry Christmas!
By Joselle, on December 13th, 2010 Cantor once remarked that the essence of mathematics lies entirely in its freedom. And it is this about mathematics that consistently inspires me. But understanding how it finds that freedom, and the relevance or meaning of what it accomplishes with it, is a deep and complex question.
And so I would like to go back to Poincare once more, as he tried to address the meaning and relevance of what could look like pure inventions in mathematics. He argues, in essence, that the mind is addressing the limitations of the senses with mathematical thinking. I’ll look today at the continuum of real numbers with him, an idea fundamental to the development of modern mathematics, and use again his text Science and Hypothesis.
In chapter two of the book, he points to the source of mathematic’s freedom:
Mathematicians do not study objects, but the relations between objects; to them it is a matter of indifference if these objects are replaced by others, provided that the relations do not change. Matter does not engage their attention, they are interested in form alone.
He is about to outline the necessity of what are called incommensurable numbers, like the square root of 2, which may be thought of a “a simple symbol,” distinguished from “a quantity which should be measurable and almost tangible.” To understand it in this way, he points out that the idea of the mathematical continuum is not “simply drawn from experiment,” and leads his reader down the following path. Appealing to a relationship between stimuli and sensation described by Fechner’s Law, one can say that an object A which weighs 10 grams and an object B which weighs 11 grams will each produce identical sensations. And the weight of B cannot be distinguished from the weight of a third object C of 12 grams. But the weight of A is readily distinguished from the weight of C. This leads to the following relation: A = B, B = C, and A < C, which he says may be regarded as “the formula of the physical continuum.” He goes on to say:
But here is an intolerable disagreement with the law of contradiction, and the necessity of banishing this disagreement has compelled us to invent the mathematical continuum. We are therefore forced to conclude that this notion has been created entirely by the mind, but it is experiment that has provided the opportunity.
He is careful to note that measurement instruments do not solve the problem since even the most delicate methods rely on the senses and so the results continue to be restricted to the physical continuum “with the contradiction which is inherent in it.” About visual characteristics he goes on to make another observation of the infinite captured by the continuum:
Nothing distinguishes a length directly observed from half that length doubled by the microscope. The whole is homgeneous to the part; and there is a fresh contradiction….The contradiction ceases as soon as the number of terms is regarded as infinite. There is nothing, for example, to prevent us from regarding the aggregate of integers as similar to the aggregate of even numbers.
This only explains the origin of continuums of what Poincare calls the first order. But a simple geometric construction can illustrate the need for adding incommensurables to this continuum.
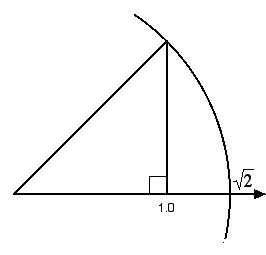
The square root of two must be on the number line.
The mathematician’s reliance on the absence of contradiction opens the door to things like non-Euclidean geometries, infinite dimensional spaces and Riemann’s very general notion of a manifold (to name a very few). It also encouraged mathematician’s to believe that logic was indeed the very foundation of mathematics. But mathematics is not built entirely on logic. It lives somewhere between thought-governed ideal realities and physical realities created by the senses. As such, it may be able to provide its own unique view of cognition itself. It may be said that cognitive processes unfold themselves into mathematical insights.
Poincare goes on to state the obvious, that the the creative power of the mind is not exhausted by the creation of the continuum. In the approaching season perhaps we can give new thought to the nature of living fictions.
By Joselle, on December 6th, 2010 It’s easy to neglect the detail of one person’s, now historic, philosophical discussion of math and science. But there is a moment, in Henri Poincare’s well known text Science and Hypothesis, that I would like to shine a light on today. The first English translation of the book was published in 1905. Chapter IV is a discussion of space and geometry and in it Poincare takes the time to make an artful distinction between our physical sense of space and mathematical space. He’s writing at a time when mathematics has successfully transgressed the restrictions of Euclidean geometry, once thought to simply be geometry. I’ve written about Riemann’s definitive contribution to the mathematical notion of ‘space’ in an earlier post. In his chapter on Space and Geometry Poincare begins with a simple statement of what is not true:
It is often said that the images we form of external objects are localized in space, and even that they can only be formed on this condition. It is also said that this space, which thus serves as a kind of framework ready prepared for our sensations and representations, is identical with the space of the geometers, having all the properties of that space.
He then summarizes the properties of a Euclidean geometrical space – that it is continuous, of three dimensions, homogeneous (i.e. all the points are identical to one another) and isotropic (identical in all directions). The interesting part of the discussion begins when he contrasts this with the properties of our sense of the space around us. He refers to this as representative space, built from visual, tactile and motor experience.
Poincare points first to the retina, a two dimensional surface and a limited framework where all of the points are not identical – all points on the retina do not play the same role. He takes particular note of the difference between points at the retina’s center and those at the edges. While this visual space may be said to be continuous, it is neither homogeneous nor isotropic. He moves away from the retina’s surface to describe our perception of a third dimension. This “reduces to a sense of the effort of accommodation which must be made, and to a sense of the convergence of the two eyes, that must take place in order to perceive an object distinctly.” Since these are muscular sensations, they are experienced differently. A complete visual space is, therefore, neither infinite, nor homogeneous nor isotropic. The question then arises: Is it, in fact, three dimensional? The mathematician takes over this argument. Since our sensation is built on at least four independent variables, two from the two-dimensional retina, and two from two kinds of distance cues, then our visual space is determined by four independently varying parameters and the complete space may be said to have four dimensions. Modern theories of the visual brain would likely say the dimension is higher. But Poincare also takes note of the fact that movement contributes to the genesis of the concept of space and argues that the sensations which correspond to movements in the same direction are only connected by an association of ideas in our minds. The aggregate of muscular sensations actually depends on as many variables as we have muscles.
Poincare summarizes his analysis in this way:
Thus we do not represent to ourselves external bodies in geometrical space, but we reason about these bodies as if they were situated in geometric space.
For Poincare, our idea of space is secondary to our experience of space which is based entirely on correlative events in our bodies.
This was a time when a mathematician would not ignore the way mathematics transgressed the boundaries of common reason and experience or would not wonder about its nature. As Poincare once said, “Though the source be obscure, still the stream flows on.” Revolutionary and far-reaching insights in both mathematics and physics were brought to the fore in the early twentieth century. And these were problematic for some. Being an early participant in the transforming ideas of modern physics Poincare writes later in the book:
When a physicist finds a contradiction between two theories which are equally dear to him, he sometimes says: “Let us not be troubled , but let us hold fast to the two ends of the chain, lest we lost the intermediate links….It is quite possible that they both express true relations, and that the contradictions only exist in the images we have formed to ourselves of our reality.
By Joselle, on November 29th, 2010 The first page of text in Morris Kline’s Mathematics and Western Culture quotes Descartes:
…..I was not surprised that many people, even of talent and scholarship, after glancing at these sciences, have either given them up as being empty and childish or, taking them to be very difficult and intricate, been deterred at the very outset from learning them…..But when I afterwards bethought myself how it could be that the earliest pioneers of Philosophy in bygone ages refused to admit to the study of wisdom any one who was not versed in Mathematics….I was confirmed in my suspicion that they had knowledge of a species of Mathematics very different from that which passes current in our time.
And ours! Part of what motivated me to create this blog is my conviction that we haven’t given mathematics the opportunity to reflect, as it does, something about ourselves, our biology and even rudimentary aspects of life itself.
Although the question of whether mathematics is something we’ve constructed or discovered can seem stale, like an overused cliche, it is still debated. And in this context I’ve wondered about generalities. Generalities are the way math ideas grow into specialized complex systems of thought – symbols for quantity grew into the real number system, an analysis of three-dimensional space grew into, among other things, infinite-dimensional vector spaces. But what does it mean to find a generality? It’s not exactly constructed. And it doesn’t only happen in mathematics. Every time we name an aggregate of objects, like trees, or dogs, insects, molecules, cells, subatomic particles, we have found some sameness among a multitude of particulars.
Today the work of Semir Zeki again got my attention again. Zeki is a neurobiologist who has worked extensively on the visual brain. He is currently a professor of Neuroesthetics at University College London and founder of the Institute of Neuroesthetics. (For some reason, word press won’t link the page for the Institute at http://neuroesthetics.org) The Institute means to establish and investigate the way art is an extension of the brain’s inherent function, which Zeki would say is to know something when faced, in every sense, with permanent change. The brain (or the body) accomplishes this with its capacity to abstract or “to emphasize the general at the expense of the particular.”
Within the Institute’s statement is the following claim:
Abstraction, which arguably is a characteristic of every one of the many different visual areas of the brain, frees the brain from enslavement to the particular and from the imperfections of the memory system.
To describe what he means by abstraction, Zeki often uses what is called orientation selectivity, the talent of many cells in the primary visual cortex to respond to lines of a certain orientation, less well to other lines, and not at all to lines orthogonal (or perpendicular) to their preferred orientation. The cells’ responses are unaffected by any particulars about the line (like color or width or context). This is a generality at the cellular level! – just a hint of what the body does.
Mathematics investigates what appear to be more conscious or more willful abstractions. Yet when scrutinized, we find more hidden within the abstraction than we started with. And these discoveries are what have made mathematics into the powerful and bewildering body of knowledge it has become.
On their web page the Institute quotes Paul Klee:
Art does not represent the visual world, it makes things visible.
Is this not what mathematics does? My interest in the biology of mathematics does not come from a reductionist tendency but more from, as Hermann Weyl says in a 1932 lecture, a desire to find the world looking “more and more as an open one, as a world not closed but pointing beyond itself.” I hope to see us break our ‘subjective’ vs. ‘objective’ habits of thought, and erase some of the boundaries we have drawn between ourselves everything else.
Zeki doesn’t address the abstractions in mathematics, but he found himself in the unexpected company of some string theorists and he wrote about the questions that came to mind in one of his blogs.
I’ll end this with another quote from Kline:
Mathematics has brought life to the dry bones of disconnected facts and, acting as connective tissue, has bound series of detached observations into bodies of science.
By Joselle, on November 22nd, 2010 The following exchange between M.P. Schutzenberger and A. Connes is lifted from the book Triangle of Thoughts:
M. P. S. — …language begins with poetry
rather than with grammar; euphony
plays a big role here.
A. C. — Your point of view coincides
with my own, since I sincerely believe
that music is at its very beginnings, like
language when it was at the stage of euphony.
I think we might succeed in this
way to educate the human mind to deal
with polyphonic situations in which several
voices coexist, in which several
states coexist, whereas our ordinary logic allows room for only one.
These words led me to wonder again about music, language and mathematics, but with an eye to music. Schutzenberger and Connes seem to be pointing to the way sound moves thought before grammar (or logic), but they caused me to wonder more generally about the overlap between music and language, and even whether mathematical intuition participates in this.
Many questions about music are yet unanswered: How is it in our nature to make music? To what extent do we share this facility with other creatures? What is melody or harmony? Does music precede language? How is it that music plays with sensations of movement, or of space, even when the body is still? While it may be said that poetry does this as well, our usual language does not. Our musical and linguistic sides are related, but they are not the same. An online article about the evolution of music and language refers to work at the Harvard Medical School where they found that:
patients who have suffered severe lesions on the left side of their brain showed that while they could not speak – no language skill as we might define it – they were able to sing phrases like “I am thirsty”, sometimes within two minutes of having the phrase mapped to a melody.
The argument was made that the persistence of some musical literacy supported the idea that it predated language. Here’s another article on language before music.
L.E.J. Brouwer, founder of the doctrine of mathematical intuitionism, writes in 1951 that the first act of intuitionism is:
Completely separating mathematics from mathematical language and hence from the phenomena of language described by theoretical logic, recognising that intuitionistic mathematics is an essentially languageless activity of the mind having its origin in the perception of a move of time. This perception of a move of time may be described as the falling apart of a life moment into two distinct things, one of which gives way to the other, but is retained by memory. If the twoity thus born is divested of all quality, it passes into the empty form of the common substratum of all twoities. And it is this common substratum, this empty form, which is the basic intuition of mathematics.
A move of time…….There isn’t time or space to explore all of the questions that come to mind when I think about the relationships between music, time, language and mathematics. But the ones I am drawn to today have primarily to do with the failure of Hilbert’s program to make logic the foundation of mathematics in the first part of the twentieth century, and the Connes quote I started with. It seems to me that logic guides mathematical perceptions, brings great clarity to them, extends their descriptive power, and is indispensable in this regard. But the music, the more fundamental experience, comes first. And Connes’ interest in “polyphonic situations” in which “several voices coexist” made me think again of modern physics, where, while doing so with precision and care, mathematics required that clear cut, this or that, expectations of physical states be abandoned in favor of the coexistence of more than one quantum mechanical state.
Mathematics and science always open doors to new experience, new sensation, new vision. But, equally revealing is to look back at ourselves, at where the vision may have come from.
By Joselle, on November 15th, 2010 In the first half of the twentieth century, physicists and mathematicians began to raise questions about what they could say about what they were actually doing. The ‘truth’ of things was beginning to elude the seekers of that truth. Both the validity of mathematical ideas and the objectivity of physics came under scrutiny. Questions about how mind and matter were related resurfaced. They led to statements like this one from Hermann Weyl’s lecture on Mind and Nature (1934):
…the structure of our scientific cognition of the world is decisively determined by the fact that this world does not exist in itself, but is merely encountered by us as an object in the correlative variance of subject and object.
In the book of selected writings where this lecture appears, there is a photo of Weyl with Hermann Hesse from 1953. Hesse’s book The Glass Bead Game, a game that employs all of the cultural and scientific knowledge of the ages, is a favorite of mine. The game is built on intellectual rigor and monastic discipline. I tried to find what I could about the relationship between Weyl and Hesse. But in my search I went astray and found instead a few accounts of another relationship, another unlikely pair, physicist Wolfgang Pauli and Carl G. Jung. In a piece by Arthur I. Miller, which highlights a dream Pauli brought to Jung, Miller looks at the dream’s relationship to Pauli’s Exclusion Principle for which he won a Nobel Prize. (Pauli and Jung are the subject of Miller’s book 137: Jung, Pauli, and the Pursuit of a Scientific Obsession)
Another take on the Pauli-Jung relationship is in an e-publication article for the Metanexus Institute which promotes transdisciplinary research into “profound questions of human meaning.” Their historical account of the meeting of Pauli and Jung is much the same. But they also let us see Pauli’s reservations about Jung.
The two met first in 1932, and Jung would be Pauli’s therapist until 1934 when Pauli ended their sessions. But two years later Pauli renewed contact with Jung. This correspondence lasted until 1957. The article quotes one of Pauli’s letters to Jung in 1937 in which he says,
even the most modern physics also lends itself to the symbolic representation of psychic processes, even down to the last detail.
Jung was convinced that number was an archetype, part of the collective unconscious, an idea he introduced that ‘psychologically’ connected the individual to the collective history of humanity. Archetypes are like hardwired organizing principles that cannot be known directly, but images of them are found in symbol. Number was the bridge, for Jung, between the human world and the higher world, believing their reality to be valid in both. Jung found, however, that he could not do mathematics and Pauli has been quoted as having said of Jung that he was “quite without scientific training.”
It was personal circumstances brought Pauli to Jung. But something about Jung’s perspective took hold in Pauli. In 1952 they published together. The English translation appeared in 1955 called The Interpretation of Nature and the Psyche. In it Pauli argues that “pure logic” is not capable of establishing a “bridge between the sense perceptions and the concepts.” (This sounds like an argument against the formalist’s hopes for finding logic to be the foundations of mathematics).
I don’t think we will find that Jung got it all right. But we will likely find that Jung got something with which philosophers of science and cognitive scientists still grapple. It has to do with the underlying significance of the body and its inexhaustible capacity to discern or characterize realities not known through the senses.
By Joselle, on November 8th, 2010 I like the word plasticity, the idea that something would be capable of being shaped or formed. It’s an optimistic word, pointing to the promise of change, or transformation (another word I like). Today I happened upon some of the work of Nancy Nersessian, Professor of Cognitive Science at the Georgia Institute of Technology. She’s written about how scientists think, or how analogies lead to conceptual breakthroughs. She uses the term generic abstraction which she defines as selectively suppressing information in a representation so as to make inferences that pertain only to the generic case. This is exactly what mathematics accomplishes as it finds the largest generalities within which particulars fit. And it accomplishes this by exploring the implications of its very carefully constructed symbolic representations.
One can see the effect of symbols moving thoughts in an early and seemingly simple step in algebra’s development. Francois Viete, a sixteenth century Frenchman, imagined writing equations using consonants to represent known quantities and vowels to represent the unknowns. He may not have done this for the first time, but he made it a popular habit. Removing the numbers was actually like pulling back the curtain for the mind’s eye. We circumvented our expectations. When you look at something like a = 5b, you may be expecting that a is some multiple of 5. But given a = xb, the lack of specifics compels a symbolic solution. We can see the potential for numeric relationships better when we take the numbers away.
In Nersessian’s study of creativity, the brain’s own plasticity is also under investigation. In the development of a generic abstraction, she speaks of hybrid analogies that go through several iterations before a working model is constructed, and in one paper in particular (“Hybrid Analogies in Conceptual Innovation in Science,” Cognitive Systems Research, Special issue 2009), she argues that visualization helps direct the iterations. All problem solving relies on the brain’s own constructive agility, and in this discussion, visualization seems to play a crucial role.
This also reminds me of the work of Samir Zeki, whose work on the visual brain was discussed in an earlier post. Rather than rewrite it let me just copy it:
He explains that abstraction is an essential characteristic “imposed upon the brain by one of its chief functions, namely the acquisition of knowledge.” Looking for the essence of things by using abstraction is what the brain is built to do. This looking for the essence, he argues, is what creative work is about.
One more thing. According to Colin Blakemore, Professor of neuroscience at the University of Oxford, the force that drove the dramatic increase in human brain size is neuroplasticity. Blakemore maintains that the change was sudden, and not accomplished by natural selection. The mutation is traced to the brain of a single early human referred to as Mitochondrial Eve!
|
|



Recent Comments