Cantor once remarked that the essence of mathematics lies entirely in its freedom. And it is this about mathematics that consistently inspires me. But understanding how it finds that freedom, and the relevance or meaning of what it accomplishes with it, is a deep and complex question.
And so I would like to go back to Poincare once more, as he tried to address the meaning and relevance of what could look like pure inventions in mathematics. He argues, in essence, that the mind is addressing the limitations of the senses with mathematical thinking. I’ll look today at the continuum of real numbers with him, an idea fundamental to the development of modern mathematics, and use again his text Science and Hypothesis.
In chapter two of the book, he points to the source of mathematic’s freedom:
Mathematicians do not study objects, but the relations between objects; to them it is a matter of indifference if these objects are replaced by others, provided that the relations do not change. Matter does not engage their attention, they are interested in form alone.
He is about to outline the necessity of what are called incommensurable numbers, like the square root of 2, which may be thought of a “a simple symbol,” distinguished from “a quantity which should be measurable and almost tangible.” To understand it in this way, he points out that the idea of the mathematical continuum is not “simply drawn from experiment,” and leads his reader down the following path. Appealing to a relationship between stimuli and sensation described by Fechner’s Law, one can say that an object A which weighs 10 grams and an object B which weighs 11 grams will each produce identical sensations. And the weight of B cannot be distinguished from the weight of a third object C of 12 grams. But the weight of A is readily distinguished from the weight of C. This leads to the following relation: A = B, B = C, and A < C, which he says may be regarded as “the formula of the physical continuum.” He goes on to say:
But here is an intolerable disagreement with the law of contradiction, and the necessity of banishing this disagreement has compelled us to invent the mathematical continuum. We are therefore forced to conclude that this notion has been created entirely by the mind, but it is experiment that has provided the opportunity.
He is careful to note that measurement instruments do not solve the problem since even the most delicate methods rely on the senses and so the results continue to be restricted to the physical continuum “with the contradiction which is inherent in it.” About visual characteristics he goes on to make another observation of the infinite captured by the continuum:
Nothing distinguishes a length directly observed from half that length doubled by the microscope. The whole is homgeneous to the part; and there is a fresh contradiction….The contradiction ceases as soon as the number of terms is regarded as infinite. There is nothing, for example, to prevent us from regarding the aggregate of integers as similar to the aggregate of even numbers.
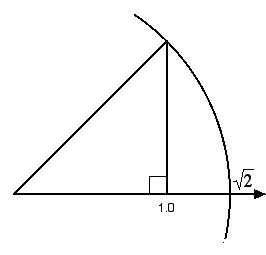
This only explains the origin of continuums of what Poincare calls the first order. But a simple geometric construction can illustrate the need for adding incommensurables to this continuum.
The square root of two must be on the number line.
The mathematician’s reliance on the absence of contradiction opens the door to things like non-Euclidean geometries, infinite dimensional spaces and Riemann’s very general notion of a manifold (to name a very few). It also encouraged mathematician’s to believe that logic was indeed the very foundation of mathematics. But mathematics is not built entirely on logic. It lives somewhere between thought-governed ideal realities and physical realities created by the senses. As such, it may be able to provide its own unique view of cognition itself. It may be said that cognitive processes unfold themselves into mathematical insights.
Poincare goes on to state the obvious, that the the creative power of the mind is not exhausted by the creation of the continuum. In the approaching season perhaps we can give new thought to the nature of living fictions.


so your last sentences seem to imply that the ‘fictions’ are in fact non-material realities, much as mathematical ideas are. is this what you mean? I like the idea that this is related to a freedom that mathematics affords.
This is exactly what I mean. But I don’t think it’s fair to say that mathematic’s characteristic freedom is just a consequence of its non-material nature. That could be misleading. I think the freedom is more a consequence of maturing symbols that remove the expectations that would otherwise limit the work of the imagination.