The idea that geometry in Gothic architecture was used to structure ideas, rather than the edifice itself, has come up before here at Mathematics Rising. But I would like to focus a bit more on this today because it illustrates something about mathematics, and mathematics’ potential, that the modern proliferation of information may be obscuring. Toward this end, I’ll begin with a quote from a paper by architect and architectural historian Nelly Shafik Ramzy published in 2015. The paper’s title is The Dual Language of Geometry in Gothic Architecture: The Symbolic Message of Euclidian Geometry versus the Visual Dialogue of Fractal Geometry.
The medieval geometry of Euclid had nothing to do with the geometry that is taught in schools today; no knowledge of mathematics or theoretical geometry of any kind was required for the construction process of medieval edifices. Using only a compass and a straight-edge, Gothic masons created myriad lace-like designs, making stone hang in the air and glass seem to chant. In a similar manner, although they did not know the recently discovered principles of Fractal geometry, Gothic artists created a style that was based on the geometry of Nature, which contains a myriad of fractal patterns.
..the paper assumes that the Gothic cathedral, with its unlimited scale, yet very detailed structure, was an externalization of a dual language that was meant to address human cognition through its details, while addressing the eye of the Divine through the overall structure, using what was thought to be the divine language of the Universe.
One of the more intriguing aspects of Ramzy’s analysis is the consideration that the brain is optimized to process fractals, suggesting that fractals are more compatible with human cognitive systems. For Ramzy, this possibility may account for the fact that Gothic artists intuitively produced fractal forms despite the absence of any scientific or mathematical basis for understanding them.
Ramzy does a fairly detailed analysis of the geometric features of a number of cathedrals at various locations.
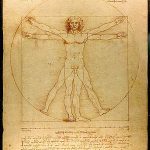 The geometrically defined proportions of the human body, for example, produced by Roman architect and engineer Marcus Vitruvius Pollio in the 1st century BC, and explored again by Leonardo da Vinci in the 15th century, are displayed in the floor plans of Florence Cathedral, as well as Reims Cathedral and Milan Cathedral. These same proportions are also found in the facades of Notre-Dame of Laon, Notre-Dame of Paris, and Amiens Cathedrals. Natural spirals that reflect the Fibonacci series can be seen in patterns that are found in San Marco, Venice, the windows of Chartres Cathedral, as well as those in San Francesco d’Assissi in Palermo, and in the carving on the pulpit of Strasburg Cathedral.
The geometrically defined proportions of the human body, for example, produced by Roman architect and engineer Marcus Vitruvius Pollio in the 1st century BC, and explored again by Leonardo da Vinci in the 15th century, are displayed in the floor plans of Florence Cathedral, as well as Reims Cathedral and Milan Cathedral. These same proportions are also found in the facades of Notre-Dame of Laon, Notre-Dame of Paris, and Amiens Cathedrals. Natural spirals that reflect the Fibonacci series can be seen in patterns that are found in San Marco, Venice, the windows of Chartres Cathedral, as well as those in San Francesco d’Assissi in Palermo, and in the carving on the pulpit of Strasburg Cathedral.
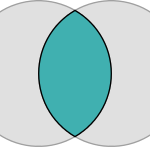 Vesica Pisces was the name given to the figure created by the intersection of two circles with the same radius in such a way that the center of each circle is on the perimeter of the other. A figure thus created has some interesting geometric properties, and was often used as a proportioning system in Gothic architecture. It can be found in the working lines of pointed arches, the plans of Beauvais Cathedral and Glastonbury Cathedral, and the facade of Amiens Cathedral. Fractal patterns are also seen in windows of Amiens, Milan, Chartres Cathedrals and Sainte-Chapelle, Paris. And the shapes of Gothic vaults are shown to reflect variations of fractal trees in Wales Cathedral, the Church of Hieronymite Monastery, Portugal, Frauenkirche, Munich and Gloucester Cathedral.
Vesica Pisces was the name given to the figure created by the intersection of two circles with the same radius in such a way that the center of each circle is on the perimeter of the other. A figure thus created has some interesting geometric properties, and was often used as a proportioning system in Gothic architecture. It can be found in the working lines of pointed arches, the plans of Beauvais Cathedral and Glastonbury Cathedral, and the facade of Amiens Cathedral. Fractal patterns are also seen in windows of Amiens, Milan, Chartres Cathedrals and Sainte-Chapelle, Paris. And the shapes of Gothic vaults are shown to reflect variations of fractal trees in Wales Cathedral, the Church of Hieronymite Monastery, Portugal, Frauenkirche, Munich and Gloucester Cathedral.
These are just a few of the observations contained in Ramzy’s paper.
And according to Ramzy:
Euclidian applications and fractal applications, geometry aimed at reproducing forms and patterns that are present in Nature, were considered to be the underpinning language of the Universe. Medieval theologians believed that God spoke through these forms and it is through such forms that they should appeal to him, thus Nature became the principal book that made the Absolute Truth visible. So, even when they applied the abstract Euclidian geometry, the Golden Mean and the proportional roots, which they found in the proportions of living forms, governed their works.
Geometric principles and mathematical ratios “were thought to be the dominant ratios of the Universe.” The viewer of these cathedrals was meant to participate in the metaphysics that was contained in its geometry.
There is an interesting interplay here of cosmological, metaphysical, and human attributes. Human body proportions are found in cathedral floor plans, for example, while God is seen as the architect of a universe whose language is grounded in mathematics. We are expected to read the universe through the cathedral. Ramzy’s reference to cognition in his discussion of fractal patterns is contained here:
Fractal Cosmology relates to the usage or appearance of fractals in the study of the cosmos. Almost anywhere one looks in the universe; there are fractals or fractal-like structures. Scientists claimed that even the human brain is optimized to process fractals, and in this sense, perception of fractals could be considered as more compatible with human cognitive system and more in tune with its functioning than Euclidian geometry. This is sometimes explained by referring to the fractal characteristics of the brain tissues, and therefore it is sometimes claimed that Euclidean shapes are at variance with some of the mathematical preferences of human brains. These theories might actually explain how Gothic artists intuitively produced fractal forms, even though they did not have the scientific basis to understand them.
It may be that these kinds of observations can help us break the categories that are now habitual in our thinking. These Gothic edifices blend our experiences of God, nature, and ourselves using mathematics. I would argue that this creates the appearance that mathematics is a kind of collective cognition. Perhaps we can find useful bridges, that connect the thoughtful and the material, if we focus on these kinds of blends, rather than on the individual disciplines into which they have evolved. Finding a way to more precisely address the relationship between our universes of ideas, and the material world we find around us, will be critical to deepening our insights across disciplinary boundaries.


Recent Comments