If one is paying attention, questions about the relationship between mathematics and reality just get more interesting. Mathematician Alain Connes is certainly the modern representation of the Platonic view that mathematical reality is a discoverable, fully existent reality. But there is also the view from MIT cosmologist Max Tegmark that our physical world is not only effectively described by mathematics but, rather, that it is a mathematical structure. And then there is the perspective of some quantum information theorists, like Vlatko Vedral, that information (defined largely by the concept of probability) is what builds the fabric of the universe. He presents this thesis in his book Decoding Reality which has recently come out in paperback. Vedral spoke about the book in an interview for The Guardian two years ago.
These ideas shift the context within which one would consider the Lakoff/Nunez view of mathematics – that it is an elaboration (through conceptual metaphor) of more fundamental experiences of the body. Mathematics, in this sense, is a purely human, body-driven cognitive tool. One of the difficulties I have had with this idea is that, while it connects mathematics to cognitive systems within us, it neglects what I think is important, namely that cognitive action can only be fully understood within the unity of a body-and-its-world. Inevitably, what we come to think about the nature of our physical reality will impact how we understand cognition as well as mathematics.
The complexity of these questions is highlighted again by articles like Bits of Reality by Tom Siegfried in Science News on April 7. Siegfried puts the birth of Vedral’s quantum information theory in place:
Quantum mechanics arose in the 1920s as the math for describing the odd behavior of atoms and electrons; information theory came along two decades later, as formulas for quantifying communication over telephone lines. For decades the two theories led separate lives in fields of study far removed from one another. While physicists expended their intellectual energy on uniting quantum mechanics with relativity (a quest that continues, still without success), information scientists graduated from telephones to computers with only occasional concern for quanta. But then in the 1980s and ’90s, quantum and information science met, married and produced offspring — specifically, the intellectual enterprise known today as quantum information theory.
Initially, quantum information snared the attention of physics fans for its possible uses in sending secret codes and creating superfast computers…But theorists pursuing quantum information’s secrets are more motivated by the quest to acquire a deeper understanding of physical reality, and perhaps to grasp more fully the nature of quantum mechanics itself.
Even in their abstraction, the contrast between the bit of computer information and the qubit of quantum information theory is interesting. Both rely on the on/off, yes/no, of the computer world’s 1’s and 0’s.
But a qubit is infused with quantum magic, allowing it be both a 1 and a 0 at the same time. This “superposition” of identities gives quantum information extraordinary power.
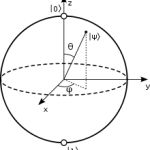
The possible states of a qubit are visualized with a sphere, the one known as a Bloch sphere. A classical bit could only be found at either the north or south pole of the sphere. But a pure qubit state could be represented by any point on its surface.
What I find interesting in this story is the relaying that seems to be happening between math and physics. Quantum mechanics is, first, the mathematics used to describe the behavior of atoms and electrons, and information theory is comprised of the formulas used to describe communication lines. But the mathematics of quantum mechanics now informs quantum information theory. And, in 1994, mathematician Peter Shor proved that a quantum computing algorithm could solve the very difficult problem of finding the prime factors of a number hundreds of digits long. According to physicist John Preskill,
Factoring is a hard problem classically, but Shor’s algorithm shows that it is an easy problem quantumly. And so it seems the boundary between what problems are hard and what problems are easy is different in our physical world — because it’s a quantum world — than it would be if the world were classical.
Siegfried notes:
Quantum information could reveal nuances about the interface between mathematics and the physical world.
And he goes on to discuss the role quantum information theory plays in efforts to identify the physical principles from which the strange rules of quantum mechanics emerge.
…in recent decades, the quest to find a physical principle from which quantum mechanics can be built has become more popular, and quantum information has been at the heart of many such efforts. Much of the work along these lines was inspired by the late physicist John Archibald Wheeler, who believed that quantum physics — and existence itself — might have its roots in aspects of information theory. His slogan “it from bit” summarized the view that reality somehow emerges from cosmic information processing.
Vlatko Vedral is one of the people who picked up that ball. Vedral defends his optimism (in a recent blog for the Huffington Post) that even if quantum physics is replaced by a new theory, only some of the arguments in his book will need revising. And there he makes the following remark:
Likewise, I argued that living systems might be using quantum physics to process information more efficiently. This too fails in the post-quantum world, which again is likely to be good news, but it might also bring a new twist on the relationship between physics and biology. Could it be, as one of the pioneers of quantum physics Erwin Schroedinger alluded a long time ago, that biology will force us to come up with new laws of physics?
-certainly.


i think quantum computer is very sound…
too esoteric for my liking…

It has always seeemd to me that quantum mechanics is not an explanation of things as much as it is an observation of things. It predicts what will (probably) happen but it does not explain how. In the quantum eraser experiment, for example, we observe that making changes to a particle located here instantly affects the behavior of another particle there, no matter how far apart the here and the there are in space. Quantum mechanics predicted that this would happen, but do we have an explanation for this? My understanding is that we do not. My understanding is that the math of quantum mechanics is not a description or an explanation of what is going on. The Feynman diagrams, for example, are not diagrams of what is physically occurring, but rather just a map that spits out the correct answers. Right? If so, it seems we have observations but no explanations, not really. Isn’t this why we have so many interpretations of quantum mechanics? Is the Copenhagen interpretation the way things are, or is it the De Broglie-Bohm interpretation? Has anyone debunked Leonard Susskind’s holographic theory? Or Seth Lloyd’s universe-as-quantum-computer theory? It just seems to me that quantum mechanics, powerful as it is, may not be capable of giving us the answers we want. Am I just not getting it, or what? I ask the professionals: are you just as dissatisfied as I am? Because if satisfaction is merely a matter of learning the math, I would be willing to do it. But it seems that the desire for the sort of satisfaction I am talking about has not been achieved, even with the math. In fact, the mystery just seems to deepen the more you dig. Yes or no? Has quantum mechanics moved us closer to an explanation, or merely revealed how very far away we really are from one?