|
|
By Joselle, on May 5th, 2017 The Riemann Hypothesis came to my attention again recently. More specifically I read a bit about the possibility that quantum mechanical measurements may provide a proof of a centuries-old hypothesis and one of mathematics’ most famous enigmas.

Within mathematics itself, without any reference to its physical meaning, the Riemann Hypothesis highlights the kind of surprises that the very notion of number itself has produced. Riemann saw a connection between a particular function of a complex variable, and the distribution of prime numbers (numbers evenly divisible by only themselves and 1). These numbers, like 2, 3, 5, 7, 11, 13, … are found among the infinite set of natural numbers. The function somehow associates information about the prime numbers (which emerge from one of the simplest arithmetic ideas) with a function that describes a relation among complex numbers. Complex numbers are represented by the sum of a real number and an imaginary number. The imaginary part of the number is a multiple of the imaginary unit i, defined as the square root of -1. The function is a zeta function, in particular it is the Riemann zeta function. It is an infinite sum (first introduced as a function of real variables by Leonhard Euler in the 18th century) whose terms are given by
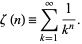
Riemann extended Euler’s idea by letting n be a complex number. With the tools of complex analysis, he found a relationship between the zeros of the zeta function, ( the n values that produced zeros) and the distribution of prime numbers. It then became possible to use these zeros to count prime numbers and to get information about their positions with respect to the natural numbers as well as to each other. Riemann discovered a formula for calculating the number of primes below a given number. It only works, however, when the real part of those complex numbers that produce zeros is 1/2. While it continues to look like the real part of all of these zeros is 1/2, there is no proof that this generalization is true. Improvements in computing programs have nonetheless made it possible to determine that it is true for at least the first 10 trillion zeros.
I should add that the Riemann zeta function fits into an intellectual weave that includes a number of other functions – ones that express related ideas or that produce specified values. This kind of close investigation of ideas, that culminates in so much mathematics, is fundamentally fueled by little more than what functions can reveal about numbers and vice versa. There are so many intriguing things about the multitude of unexpected results produced by these purely abstract investigations. Yet the nature of this wholly symbolic exploration rarely shows up in discussions of science in general, or of cognition and epistemology in particular. When we dig further into the world of numbers and their relations, (and find so much!) what are we actually looking at? Whether we’re looking at our ourselves or at an ideal world that is inaccessible to our senses, it is equally remarkable that we can see it at all. I feel strongly that mathematics is particularly fertile ground for planting epistemological questions.
The Riemann zeta function is known for being able to answer questions about the spacing or distribution of prime numbers. And prime numbers are important to the creation of new encryption algorithms that rely on them. But the zeta function has also found application in the physical side of our experience – in things like quantum statistical mechanics and nuclear physics.
The natural fit that the Riemann zeta function enjoys in physics is even more surprising. On the School of Mathematics website at the University of Bristol is this:
The University of Bristol has been at the forefront of showing that there are striking similarities between the Riemann zeros and the quantum energy levels of classically chaotic systems.
From a conference in 1996 in Seattle, aimed at fostering collaboration between physicists and number theorists, came early evidence of correlation between the arrangement of the Riemann zeroes and the energy levels of quantum chaotic systems. If this were true it would prove the Riemann hypothesis.
This is a reversal of what usually happens. Mathematical discoveries usually contribute to physical discoveries and not the other way around. But observations in physics have moved so far outside the range of the senses that physicists necessarily rely more and more heavily on mathematical structure. The disciplines, are inevitably more and more entangled.
Natalie Wolchover wrote about these efforts in a recent Quanta Magazine article.
As mathematicians have attacked the hypothesis from every angle, the problem has also migrated to physics. Since the 1940s, intriguing hints have arisen of a connection between the zeros of the zeta function and quantum mechanics. For instance, researchers found that the spacing of the zeros exhibits the same statistical pattern as the spectra of atomic energy levels. In 1999, the mathematical physicists Michael Berry and Jonathan Keating, building on an earlier conjecture of David Hilbert and George Pólya, conjectured that there exists a quantum system (that is, a system with a position and a momentum that are related by Heisenberg’s uncertainty principle) whose energy levels exactly correspond to the nontrivial zeros of the Riemann zeta function…
If such a quantum system existed, this would automatically imply the Riemann hypothesis.
Wolchover explains that physicists who have their eye on the prize are exploring quantum systems described by matrices whose eigenvalues correspond to the system’s energy levels. A recent paper in Physical Review Letters, authored by Carl Bender of Washington University in St. Louis, Dorje Brody of Brunel University London and Markus Müller of the University of Western Ontario proposed a candidate system.
If physicists do someday nail down the quantum interpretation of the zeros of the zeta function,… this could provide an even more precise handle on the prime numbers than Riemann’s formula does, since matrix eigenvalues follow very well-understood statistical distributions. It would have other implications as well…
A quantum system that models the distribution of primes might provide a simple model of chaos. This narrative is a nice story about the insightful nature of mathematics – about the way it can see in.
By Joselle, on March 24th, 2017 The idea that geometry in Gothic architecture was used to structure ideas, rather than the edifice itself, has come up before here at Mathematics Rising. But I would like to focus a bit more on this today because it illustrates something about mathematics, and mathematics’ potential, that the modern proliferation of information may be obscuring. Toward this end, I’ll begin with a quote from a paper by architect and architectural historian Nelly Shafik Ramzy published in 2015. The paper’s title is The Dual Language of Geometry in Gothic Architecture: The Symbolic Message of Euclidian Geometry versus the Visual Dialogue of Fractal Geometry.
The medieval geometry of Euclid had nothing to do with the geometry that is taught in schools today; no knowledge of mathematics or theoretical geometry of any kind was required for the construction process of medieval edifices. Using only a compass and a straight-edge, Gothic masons created myriad lace-like designs, making stone hang in the air and glass seem to chant. In a similar manner, although they did not know the recently discovered principles of Fractal geometry, Gothic artists created a style that was based on the geometry of Nature, which contains a myriad of fractal patterns.
..the paper assumes that the Gothic cathedral, with its unlimited scale, yet very detailed structure, was an externalization of a dual language that was meant to address human cognition through its details, while addressing the eye of the Divine through the overall structure, using what was thought to be the divine language of the Universe.
One of the more intriguing aspects of Ramzy’s analysis is the consideration that the brain is optimized to process fractals, suggesting that fractals are more compatible with human cognitive systems. For Ramzy, this possibility may account for the fact that Gothic artists intuitively produced fractal forms despite the absence of any scientific or mathematical basis for understanding them.
Ramzy does a fairly detailed analysis of the geometric features of a number of cathedrals at various locations.
 The geometrically defined proportions of the human body, for example, produced by Roman architect and engineer Marcus Vitruvius Pollio in the 1st century BC, and explored again by Leonardo da Vinci in the 15th century, are displayed in the floor plans of Florence Cathedral, as well as Reims Cathedral and Milan Cathedral. These same proportions are also found in the facades of Notre-Dame of Laon, Notre-Dame of Paris, and Amiens Cathedrals. Natural spirals that reflect the Fibonacci series can be seen in patterns that are found in San Marco, Venice, the windows of Chartres Cathedral, as well as those in San Francesco d’Assissi in Palermo, and in the carving on the pulpit of Strasburg Cathedral. The geometrically defined proportions of the human body, for example, produced by Roman architect and engineer Marcus Vitruvius Pollio in the 1st century BC, and explored again by Leonardo da Vinci in the 15th century, are displayed in the floor plans of Florence Cathedral, as well as Reims Cathedral and Milan Cathedral. These same proportions are also found in the facades of Notre-Dame of Laon, Notre-Dame of Paris, and Amiens Cathedrals. Natural spirals that reflect the Fibonacci series can be seen in patterns that are found in San Marco, Venice, the windows of Chartres Cathedral, as well as those in San Francesco d’Assissi in Palermo, and in the carving on the pulpit of Strasburg Cathedral.
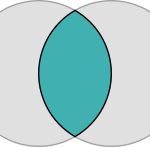 Vesica Pisces was the name given to the figure created by the intersection of two circles with the same radius in such a way that the center of each circle is on the perimeter of the other. A figure thus created has some interesting geometric properties, and was often used as a proportioning system in Gothic architecture. It can be found in the working lines of pointed arches, the plans of Beauvais Cathedral and Glastonbury Cathedral, and the facade of Amiens Cathedral. Fractal patterns are also seen in windows of Amiens, Milan, Chartres Cathedrals and Sainte-Chapelle, Paris. And the shapes of Gothic vaults are shown to reflect variations of fractal trees in Wales Cathedral, the Church of Hieronymite Monastery, Portugal, Frauenkirche, Munich and Gloucester Cathedral. Vesica Pisces was the name given to the figure created by the intersection of two circles with the same radius in such a way that the center of each circle is on the perimeter of the other. A figure thus created has some interesting geometric properties, and was often used as a proportioning system in Gothic architecture. It can be found in the working lines of pointed arches, the plans of Beauvais Cathedral and Glastonbury Cathedral, and the facade of Amiens Cathedral. Fractal patterns are also seen in windows of Amiens, Milan, Chartres Cathedrals and Sainte-Chapelle, Paris. And the shapes of Gothic vaults are shown to reflect variations of fractal trees in Wales Cathedral, the Church of Hieronymite Monastery, Portugal, Frauenkirche, Munich and Gloucester Cathedral.
These are just a few of the observations contained in Ramzy’s paper.
And according to Ramzy:
Euclidian applications and fractal applications, geometry aimed at reproducing forms and patterns that are present in Nature, were considered to be the underpinning language of the Universe. Medieval theologians believed that God spoke through these forms and it is through such forms that they should appeal to him, thus Nature became the principal book that made the Absolute Truth visible. So, even when they applied the abstract Euclidian geometry, the Golden Mean and the proportional roots, which they found in the proportions of living forms, governed their works.
Geometric principles and mathematical ratios “were thought to be the dominant ratios of the Universe.” The viewer of these cathedrals was meant to participate in the metaphysics that was contained in its geometry.
There is an interesting interplay here of cosmological, metaphysical, and human attributes. Human body proportions are found in cathedral floor plans, for example, while God is seen as the architect of a universe whose language is grounded in mathematics. We are expected to read the universe through the cathedral. Ramzy’s reference to cognition in his discussion of fractal patterns is contained here:
Fractal Cosmology relates to the usage or appearance of fractals in the study of the cosmos. Almost anywhere one looks in the universe; there are fractals or fractal-like structures. Scientists claimed that even the human brain is optimized to process fractals, and in this sense, perception of fractals could be considered as more compatible with human cognitive system and more in tune with its functioning than Euclidian geometry. This is sometimes explained by referring to the fractal characteristics of the brain tissues, and therefore it is sometimes claimed that Euclidean shapes are at variance with some of the mathematical preferences of human brains. These theories might actually explain how Gothic artists intuitively produced fractal forms, even though they did not have the scientific basis to understand them.
It may be that these kinds of observations can help us break the categories that are now habitual in our thinking. These Gothic edifices blend our experiences of God, nature, and ourselves using mathematics. I would argue that this creates the appearance that mathematics is a kind of collective cognition. Perhaps we can find useful bridges, that connect the thoughtful and the material, if we focus on these kinds of blends, rather than on the individual disciplines into which they have evolved. Finding a way to more precisely address the relationship between our universes of ideas, and the material world we find around us, will be critical to deepening our insights across disciplinary boundaries.
By Joselle, on February 28th, 2017

Both Quanta Magazine and New Scientist reported on some renewed interest in an old idea. It was an approach to particle physics, proposed by theoretical physicist Geoffrey Chew in the 1960s, that ignored questions about which particles were most elementary and put a major portion of the weight of discovery on mathematics. Chew expected that information about the strong interaction could be derived from looking at what happens when particles of any sort collide. And he proposed S-matrix theory as a substitute for quantum field theory. S-matrix theory contained no notion of space and time. These were replaced by the abstract mathematical properties of the S-matrix, which had been developed by Werner Heisenberg in 1943 as a principle of particle interactions.
New research, with a similarly democratic approach to matter, is concerned with mathematically modeling phase transitions – those moments when matter undergoes a significant transformation. The hope is that what is learned about phase transitions could tell us quite a lot about the fundamental nature of all matter. As New Scientist author, Gabriel Popkin, tells us:
Whether it’s the collective properties of electrons that make a material magnetic or superconducting, or the complex interactions by which everyday matter acquires mass, a host of currently intractable problems might all follow the same mathematical rules. Cracking this code could help us on the way to everything from more efficient transport and electronics to a new, shinier, quantum theory of gravity.
Toward this end, in 1944, Norwegian physicist Lars Onsager solved the problem of modeling material that loses magnetism when heated above a certain temperature. While his was a 2-dimensional model, it has none-the-less been used to simulate the flipping of various physical states from the spread of an infectious disease to neuron signaling in the brain. It’s referred to as the Ising model, named for Ernst Ising, who first investigated the idea in his PhD thesis but without success.
In the 1960s, Russian theorist Alexander Polyakov began studying how fundamental particle interactions might undergo phase transitions, motivated by the fact that the 2D Ising model, and the equations that describe the behavior of elementary particles, shared certain symmetries. And so he worked backwards from the symmetries to the equations.
Popkin explains:
Polyakov’s approach was certainly a radical one. Rather than start out with a sense of what the equations describing the particle system should look like, Polyakov first described its overall symmetries and other properties required for his model to make mathematical sense. Then, he worked backwards to the equations. The more symmetries he could describe, the more he could constrain how the underlying equations should look.
Polyakov’s technique is now known as the bootstrap method, characterized by its ability to pull itself up by its own bootstraps and generate knowledge from only a few general properties. “You get something out of nothing,” says Komargodski. Polyakov and his colleagues soon managed to bootstrap their way to replicating Onsager’s achievement with the 2D Ising model – but try as they might, they still couldn’t crack the 3D version. “People just thought there was no hope,” says David Poland, a physicist at Yale University. Frustrated, Polyakov moved on to other things, and bootstrap research went dormant.
This is part of the old idea. Bootstrapping, as a strategy, is attributed to Geoffrey Chew who, in the 1960’s, argued that the laws of nature could be deduced entirely from the internal demand that they be self-consistent. In Quanta, Natalie Wolchover explains:
Chew’s approach, known as the bootstrap philosophy, the bootstrap method, or simply “the bootstrap,” came without an operating manual. The point was to apply whatever general principles and consistency conditions were at hand to infer what the properties of particles (and therefore all of nature) simply had to be. An early triumph in which Chew’s students used the bootstrap to predict the mass of the rho meson — a particle made of pions that are held together by exchanging rho mesons — won many converts.
The effort gained greater traction again in 2008 when physicist Slava Rychkov and colleagues at CERN decided to use these methods to build a physics theory that didn’t have a Higgs particle. This turned out not to be necessary (I suppose), but the work was productive none-the-less in the development of bootstrapping techniques.
The symmetries of physical systems at critical points are transformations that, when applied, leave the system unchanged. Particularly important are scaling symmetries, where zooming in or out doesn’t change what you see, and conformal symmetries where the shapes of things are preserved under transformations. The key to Polykov’s work was to realize that different materials, at critical points, have symmetries in common. These bootstrappers are exploring a mathematical theory space, and they seem to be finding that the set of all quantum field theories forms a unique mathematical structure.
What’s most interesting about all of this is that these physicists are investigating the geometry of a ‘theory space,” where theories live, and where the features of theories can be examined. Nima Arkani-Hamed, Professor of physics at the Institute for Advanced Study has suggested that the space they are investigating could have a polyhedral structure with interesting theories living at the corners. It was also suggested that the polyhedral might encompass the amplituhedron – a geometric object discovered in 2013 that encodes, in its volume, the probabilities of different particle collision outcomes.
Wolchover wrote about the amplituhedron in 2013.
The revelation that particle interactions, the most basic events in nature, may be consequences of geometry significantly advances a decades-long effort to reformulate quantum field theory, the body of laws describing elementary particles and their interactions. Interactions that were previously calculated with mathematical formulas thousands of terms long can now be described by computing the volume of the corresponding jewel-like “amplituhedron,” which yields an equivalent one-term expression.
The decades-long effort is the one to which Chew also contributed. The discovery of the amplituhedron began when some mathematical tricks were employed to calculate the scattering amplitudes of known particle interactions, and theorists Stephen Parke and Tomasz Taylor found a one term expression that could do the work of hundreds of Feynman diagrams that would translate into thousands of mathematical terms. It took about 30 years for the patterns being identified in these simplified expressions to be recognized as the volume of a new mathematical object, now named the amplituhedron. Nima Arkani-Hamed and Jaroslav Trinka published results in 2014.
Again from Wolchover:
Beyond making calculations easier or possibly leading the way to quantum gravity, the discovery of the amplituhedron could cause an even more profound shift, Arkani-Hamed said. That is, giving up space and time as fundamental constituents of nature and figuring out how the Big Bang and cosmological evolution of the universe arose out of pure geometry.
Whatever the future of these ideas, there is something inspiring about watching the mind’s eye find clarifying geometric objects in a sea of algebraic difficulty. The relationship between mathematics and physics, or mathematics and material for that matter, is a consistently beautiful, captivating, and enigmatic puzzle.
By Joselle, on January 31st, 2017 Not too long ago I wrote about entropy, and what has come to be known as Maxwell’s demon – a hypothetical creature, invented in 1871 by James Clark Maxwell. The creature was the product of a thought experiment meant to explore the possibility of violating the second law of thermodynamics using information to impede entropy (otherwise known as the gradual but inevitable decline of everything into disorder). The only reason the demon succeeds in stopping the gradual decline of order is that it has information that can be used to rearrange the behavior of molecules, information that we cannot acquire from out perspective. That post was concerned with the surprising reality of such a creature, as physicists have now demonstrated that it could be made physical, even mechanical, in the form of an information heat engine or in the action of light beams.
I read about the demon again today in a Quanta Magazine article, How Life (and Death) Spring Fr0m Disorder. Much of the focus of this article concerns understanding evolution from a computational point of view. But author Philip Ball describes Maxwell’s creature and how it impedes entropy, since it is this action against entropy that is the key to this new and interesting approach to biology, and to evolution in particular.
Once we regard living things as agents performing a computation — collecting and storing information about an unpredictable environment — capacities and considerations such as replication, adaptation, agency, purpose and meaning can be understood as arising not from evolutionary improvisation, but as inevitable corollaries of physical laws. In other words, there appears to be a kind of physics of things doing stuff, and evolving to do stuff. Meaning and intention — thought to be the defining characteristics of living systems — may then emerge naturally through the laws of thermodynamics and statistical mechanics.
In 1944, Erwin Schrödinger approached this idea by suggesting that living organisms feed on what he called negative entropy. And this is exactly what this new research is investigating – namely the possibility that organisms behave in a way that keeps them out of equilibrium, by exacting work from the environment with which they are correlated, and this is done by using information that they share with that environment (as the demon does). Without using this information, entropy, or the second law of thermodynamics, would govern the gradual decline of the organism into disorder and it would die. Schrödinger’s hunch went so far as to propose that organisms achieve this negative entropy by collecting and storing information. Although he didn’t know how, he imagined that they somehow encoded the information and passed it on to future generations. But converting information from one form to another is not cost free. Memory storage is finite and erasing information to gather new information will cause the dissipation of energy. Managing the cost becomes one of the functions of evolution.
According to David Wolpert, a mathematician and physicist at the Santa Fe Institute who convened the recent workshop, and his colleague Artemy Kolchinsky, the key point is that well-adapted organisms are correlated with that environment. If a bacterium swims dependably toward the left or the right when there is a food source in that direction, it is better adapted, and will flourish more, than one that swims in random directions and so only finds the food by chance. A correlation between the state of the organism and that of its environment implies that they have information in common. Wolpert and Kolchinsky say that it’s this information that helps the organism stay out of equilibrium — because, like Maxwell’s demon, it can then tailor its behavior to extract work from fluctuations in its surroundings. If it did not acquire this information, the organism would gradually revert to equilibrium: It would die.
Looked at this way, life can be considered as a computation that aims to optimize the storage and use of meaningful information. And life turns out to be extremely good at it.
This correlation between an organism and its environment is reminiscent of the structural coupling introduced by biologist H.R. Maturana which he characterizes in this way: “The relation between a living system and the medium in which it exists is a structural one in which living system and medium change together congruently as long as they remain in recurrent interactions.”
And these ideas do not dismiss the notion of natural selection. Natural selection is just seen as largely concerned with minimizing the cost of computation. The implications of this perspective are compelling. Jeremy England at the Massachusetts Institute of Technology has applied this notion of adaptation to complex, nonliving systems as well.
Complex systems tend to settle into these well-adapted states with surprising ease, said England: “Thermally fluctuating matter often gets spontaneously beaten into shapes that are good at absorbing work from the time-varying environment.”
Working from the perspective of a general physical principle –
If replication is present, then natural selection becomes the route by which systems acquire the ability to absorb work — Schrödinger’s negative entropy — from the environment. Self-replication is, in fact, an especially good mechanism for stabilizing complex systems, and so it’s no surprise that this is what biology uses. But in the nonliving world where replication doesn’t usually happen, the well-adapted dissipative structures tend to be ones that are highly organized, like sand ripples and dunes crystallizing from the random dance of windblown sand. Looked at this way, Darwinian evolution can be regarded as a specific instance of a more general physical principle governing nonequilibrium systems.
This is an interdisciplinary effort that brings to mind a paper by Virginia Chaitin which I discussed in another post. The kind of interdisciplinary work that Chaitin is describing, involves the adoption of a new conceptual framework, borrowing the very way that understanding is defined within a particular discipline, as well as the way it is explored and the way it is expressed in that discipline. Here we have the confluence of thermodynamics and Darwinian evolution made possible with the mathematical study of information. And I would caution readers of these ideas not to assume that the direction taken by this research reduces life to the physical laws of interactions. It may look that way at first glance. But I would suggest that the direction these ideas are taking is more likely to lead to a broader definition of life. In fact there was a moment when I thought I heard the echo of Leibniz’s monads.
You’d expect natural selection to favor organisms that use energy efficiently. But even individual biomolecular devices like the pumps and motors in our cells should, in some important way, learn from the past to anticipate the future. To acquire their remarkable efficiency, Still said, these devices must “implicitly construct concise representations of the world they have encountered so far, enabling them to anticipate what’s to come.”
It’s not possible to do any justice to the nature of the fundamental, living, yet non-material substance that Leibniz called monads, but I can, at the very least, point to a a few things about them. Monads exist as varying states of perception (though not necessarily conscious perceptions). And perceptions in this sense can be thought of as representations or expressions of the world or, perhaps, as information. He describes a heirarchy of functionality among them. Ones mind, for example, has clearer perceptions (or representations) than those contained in the monads that make up other parts of the body. But, being a more dominant monad, ones mind contains ‘the reasons’ for what happens in the rest of the body. And here’s the idea that came to mind in the context of this article. An individual organ contains ‘the reasons’ for what happens in its cells, and a cell contains ‘the reasons’ for what happens in its organelles. The cell has its own perceptions or representations. I don’t have a way to precisely define ‘the reasons,’ but like the information-driven states of nonequilibrium being considered by physicists, biologists, and mathematicians, this view of things spreads life out.
By Joselle, on December 31st, 2016 I could go on for quite some time about the difference between dreaming and being awake. I could see myself picking carefully through every thought I have ever had about the significance of dreams, and I know I would end up with a proliferation of questions, rather than a clarification of anything. But I think that this is how it should be. We understand so little about our awareness, our consciousness, and what cognitive processes actually produce for us. All of this comes to mind, at the moment, because I just read an article in Plus Magazine based on a press conference given by Andrew Wiles at the Heidelberg Laureate Forum in September 2016. Wiles, of course, is famous for having proved Fermat’s Last Theorem in 1995. The article highlights some of Wiles’ thoughts about what it’s like to do mathematics, and what it feels like when he’s doing it. When asked about whether he could feel when a mathematical investigation was headed in the right direction, or when things were beginning to ‘harmonize,’ he said
Yes, absolutely. When you get it, it’s like the difference between dreaming and being awake.
If I had the opportunity, I would ask him to explain this a bit because the relationship between dream sensations and waking sensations has always been interesting to me. The relationship between language and brain imagery, for example, is intriguing. I once had a dream in which someone very close to me looked transparent. I could see through him, and I actually said those words in the dream. I would learn, in due time, that this person was not entirely who he appeared to be. But what Wiles seems to be addressing is the clarity and the certainty of being awake, of opening ones eyes, in contrast to the sometimes enigmatic narrative of a dream. This is what it feels like when you begin to find an idea.
Wiles also had a refreshingly simple response to a question about whether mathematics is invented or discovered:
To tell you the truth, I don’t think I know a mathematician who doesn’t think that it’s discovered. So we’re all on one side, I think. In some sense perhaps the proofs are created because they’re more fallible and there are many options, but certainly in terms of the actual things we find we just think of it as discovered.
I’m not sure if the next question in the article was meant as a challenge to what Wiles believes about mathematical discovery, but it seems posed to suggest that the belief held by mathematicians that they are discovering things is a necessary illusion, something they need to believe in order to do the work they’re doing. And to this possibility Wiles says,
I wouldn’t like to say it’s modesty but somehow you find this thing and suddenly you see the beauty of this landscape and you just feel it’s been there all along. You don’t feel it wasn’t there before you saw it, it’s like your eyes are opened and you see it. (emphasis added)
And this is the key I think, “it’s like your eyes are opened and you see it.” Cognitive neuroscientists involved in understanding vision have described the physical things we see as ‘inventions’ of the visual brain. This is because what we see is pieced together from the visual attributes of objects we perceive (shape, color, movement, etc.), attributes processed by particular cells, together with what looks like the computation of probabilities based on previous visual experience. I believe that questions about how the brain organizes sensation, and questions about what it is that the mathematician explores, are undoubtedly related. Trying to describe the sensation of ‘looking’ in mathematics (as opposed to the formal reasoning that is finally written down) Wiles says this:
…it’s extremely creative. We’re coming up with some completely unexpected patterns, either in our reasoning or in the results. Yes, to communicate it to others we have to make it very formal and very logical. But we don’t create it that way, we don’t think that way. We’re not automatons. We have developed a kind of feel for how it should fit together and we’re trying to feel, “Well, this is important, I haven’t used this, I want to try and think of some new way of interpreting this so that I can put it into the equation,” and so on.
I think it’s important to note that Wiles is telling us that the research mathematician will come up with some completely unexpected patterns in either their reasoning or their results. The unexpected patterns in the results are what everyone gets to see. But that one would find unexpected patterns in ones reasoning is particularly interesting. And clearly the reasoning and the results are intimately tied.
Like the sound that is produced from the numbers associated with the marks on a page of music, there is the perceived layer of mathematics about which mathematicians are passionate. And this is the thing about which it is very difficult to speak. Yet the power of what this perceived layer is may only be hinted at by the proliferation of applications of mathematical ideas in every area of our lives.
Best wishes for the New Year!
By Joselle, on November 30th, 2016 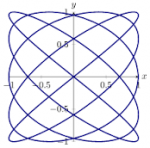
Roger Antonsen came to my attention with a TED talk recorded in 2015 that was posted in November. Characterized by the statement, “Math is the hidden secret to understanding the world,” it piqued my curiosity. Antonsen is an associate professor in the Department of Informatics at the University of Oslo. Informatics has been defined as the science of information and computer information systems but its broad reach appears to be related to the proliferation of ideas in computer science, physics, and biology that spring from information-based theories. The American Medical Informatics Association (AMIA) describes the science of informatics as:
…inherently interdisciplinary, drawing on (and contributing to) a large number of other component fields, including computer science, decision science, information science, management science, cognitive science, and organizational theory.
Antonsen describes himself as a logician, mathematician, and computer scientist, with research interests in proof theory, complexity theory, automata, combinatorics and the philosophy of mathematics. His talk, however, was focused on how mathematics reflects the essence of understanding, where mathematics is defined as the science of patterns, and the essence of understanding is defined as the ability to change one’s perspective. In this context, pattern is taken to be connected structure or observed regularity. But Antonsen highlights the important fact that mathematics assigns a language to these patterns. In mathematics, patterns are captured in a symbolic language and equivalences show us the relationship between two points of view. Equalities, Antonsen explains, show us ‘different perspectives’ on the same thing.
In his exploration of the many ways to represent concepts, Antonsen’s talk brought questions to mind that I think are important and intriguing. For example. what is our relationship to these patterns, some of which are ubiquitous? How is it that mathematics finds them? What causes them to emerge in the purely abstract, introspective world of the mathematician? Using numbers, graphics, codes, and animated computer graphics, he demonstrated, for example, the many representations of 4/3. And after one of those demonstrations, he received unexpected applause. The animation showed two circles with equal radii, and a point rotating clockwise on each of the circles but at different rates – one moved exactly 4/3 times as fast as the other. The circles lined up along a diagonal. The rotating point on each circumference was then connected to a line whose endpoint was another dot. The movement of this third dot looked like it was just dancing around until we were shown that it was tracing a pleasing pattern. The audience was clearly pleased with this visual surprise. (FYI, this particular demonstration happens about eight and a half minutes in) Antonsen didn’t expect the applause, and added quickly that what he had shown was not new, that it was known. He explains in his footnotes:
This is called a Lissajous curve and can be created in many different ways, for example with a harmonograph.
These curves emerge from periodicity, like the curves for sine and cosine functions and their related unit circle expressions. In fact it is the difference in the periods described by the rotation of the point around each of Antonsen’s circles (a period being one full rotation) that produced the curve that so pleased his audience.
I believe that Antonsen wanted to make the point that because mathematics brings a language to all of the patterns that emerge from sensation, and because it is driven by the directive that there is always value in finding new points of view, mathematics is a kind of beacon for understanding, everything. About this I wholeheartedly agree. I have always found comfort in the hopefulness associated with finding another point of view, and the powerful presence of this drive in mathematics may be the root of what captivates me about it. Mathematics makes very clear that there is no limit to the possibilities for creative and careful thought.
But I also think that the way Antonsen’s audience enjoyed a very mathematical thing deserves some comment. They didn’t see the mathematics, but they saw one of the things that the mathematics is about – a shape, a pattern, that emerges from relationship. And their impulse was to applaud. This tells us something about what we are not accomplishing in most of our math classes.
By Joselle, on October 31st, 2016 When I read the subheading in a recent Scientific American article, it brought me back to some 18th century thoughts which I recently reviewed. The subheading of a piece by Clara Moskowitz’s that describes a new effort in theoretical physics reads:
Hundreds of researchers in a collaborative project called “It from Qubit” say space and time may spring up from the quantum entanglement of tiny bits of information
This sounds like our physical world emerged from interactions among things that are not physical – namely tiny bits of information. And it reminded me of the logical and physical constraints that led Wilhelm Gottfried Leibniz to his view that the fundamental substance of the universe is more like a mathematical point than a tiny particle. Leibniz’s analysis of the physical world rested, not on measurement, but on mathematical thought. He rejected the widely accepted belief that all matter was an arrangement of indivisible, fundamental materials, like atoms. Atoms would be hard, Leibniz argued, and so collisions between atoms would be abrupt, resulting in discontinuous changes in nature. The absence of abrupt changes in nature indicated to him that all matter, regardless of how small, possessed some elasticity. Since elasticity required parts, Leibniz concluded that all material objects must be compounds, amalgams of some sort. Then the ultimate constituents of the world, in order to be simple and indivisible, must be without extension or without dimension, like a mathematical point. For Leibniz, the universe of extended matter is actually a consequence of these simple non-material substances.
This is not exactly the direction being taken by the physicists in Moskowitz’s article, but there is something that these views, separated by centuries, share. And while Moskowitz doesn’t do a lot to clarify the nature of quantum information, I believe the article addresses important shifts in the strategies of theoretical physicists.
The notion that spacetime has bits or is “made up” of anything is a departure from the traditional picture according to general relativity. According to the new view, spacetime, rather than being fundamental, might “emerge” via the interactions of such bits. What, exactly, are these bits made of and what kind of information do they contain? Scientists do not know. Yet intriguingly, “what matters are the relationships” between the bits more than the bits themselves, says IfQ collaborator Brian Swingle, a postdoc at Stanford University. “These collective relationships are the source of the richness. Here the crucial thing is not the constituents but the way they organize together.”
In discussions of his own work on Constructor Theory, David Deutsch often corrects the somewhat self-centered view, born of our experience with words and ideas, that information is not physical. In a piece I wrote about Deutsch’s work, the nature of information is underscored.
Information is “instantiated in radically different physical objects that obey different laws of physics.” In other words, information becomes represented by an instance, or an occurrence, like the attribute of a creature determined by the information in its DNA…Constructor theory is meant to get at what Deutsch calls this “substrate independence of information,” which necessarily involves a more fundamental level of physics than particles, waves and space-time. And he suspects that this ‘more fundamental level’ may be shared by all physical systems.
This move toward information-based physical theories will likely break some of our habits of thought, unveil the prejudice in our perspectives, that have developed over the course of our scientific successes. New understanding requires some struggle with the very way that we think and organize our world. And wrestling with the nature of information, what it is and what it does, has the potential to be very useful in clearing new paths.
Because the project involves both the science of quantum computers and the study of spacetime and general relativity, it brings together two groups of researchers who do not usually tend to collaborate: quantum information scientists on one hand and high-energy physicists and string theorists on the other. “It marries together two traditionally different fields: how information is stored in quantum things and how information is stored in space and time,” says Vijay Balasubramanian, a physicist at the University of Pennsylvania who is an IfQ principal investigator.
In his 2008 Provisional Manifesto Giulio Tononi finds experience to be the mathematical shape taken on by integrated information. He proposes a way to characterize experience using a geometry that describes informational relationships. One could say he proposes, essentially, a model for describing conscious experience. But Tononi himself blurs this distinction between the model and the reality when he writes that these shapes are:
…often morphing smoothly into another shape as new informational relationships are specified through its mechanisms entering new states. Of course, we cannot dream of visualizing such shapes as qualia diagrams (we have a hard time with shapes generated by three elements). And yet, from a different perspective, we see and hear such shapes all the time, from the inside, as it were, since such shapes are actually the stuff our dreams are made of— indeed the stuff all experience is made of.
These things don’t make some common sense, and there is some resistance to all of them. But it is that ‘common sense’ that contains all of our thinking and perceiving habits, all of our prejudices. Neuroscientist Christof Koch is a proponent of Tononi’s theory of consciousness which implies that there is some level of consciousness in everything. And here’s an example of the resistance from John Horgan’s blog Cross Check
That brings me to arguably the most significant development of the last two decades of research on the mind-body problem: Koch, who in 1994 resisted the old Chalmers information conjecture, has embraced integrated information theory and its corollary, panpsychism. Koch has suggested that even a proton might possess a smidgeon of proto-consciousness. I equate the promotion of panpsychism by Koch, Tononi, Chalmers and other prominent mind-theorists to the promotion of multiverse theories by leading physicists. These are signs of desperation, not progress.
I couldn’t disagree more.
By Joselle, on September 30th, 2016 An article published in May in Quanta Magazine had the following remark as its lead:
A surprising new proof is helping to connect the mathematics of infinity to the physical world.
My first thought was that the mathematics of infinity is already connected to the physical world. But Natalie Wolchover’s opening few paragraphs were inviting:
With a surprising new proof, two young mathematicians have found a bridge across the finite-infinite divide, helping at the same time to map this strange boundary.
The boundary does not pass between some huge finite number and the next, infinitely large one. Rather, it separates two kinds of mathematical statements: “finitistic” ones, which can be proved without invoking the concept of infinity, and “infinitistic” ones, which rest on the assumption — not evident in nature — that infinite objects exist.
Mapping and understanding this division is “at the heart of mathematical logic,” said Theodore Slaman, a professor of mathematics at the University of California, Berkeley. This endeavor leads directly to questions of mathematical objectivity, the meaning of infinity and the relationship between mathematics and physical reality.
It is becoming increasingly clear to me that harmonizing the finite and the infinite has been an almost ever-present human enterprise, at least as old as the earliest mythical descriptions of the worlds we expected to find beyond the boundaries of the day-to-day, worlds that were below us or above us, but not confined, not finite. I have always been provoked by the fact that mathematics found greater precision with the use of the notion of infinity, particularly in the more concept-driven mathematics of the 19th century, in real analysis and complex analysis. Understanding infinities within these conceptual systems cleared productive paths in the imagination. These systems of thought are at the root of modern physical theories. Infinite dimensional spaces extend geometry and allow topology. And finding the infinite perimeters of fractals certainly provides some reconciliation of the infinite and the finite, with the added benefit of ushering in new science.
Within mathematics, the questionable divide between the infinite and the finite seems to be most significant to mathematical logic. Wolchover’s article addresses work related to Ramsey theory, a mathematical study of order in combinatorial mathematics, a branch of mathematics concerned with countable, discrete structures. It is the relationship of a Ramsey theorem to a system of logic whose starting assumptions may or may not include infinity that sets the stage for its bridging potential. While the theorem in question is a statement about infinite objects, it has been found to be reducible to the finite, being equivalent in strength to a system of logic that does not rely on infinity.
Wolchover published another piece about disputes among mathematicians about the nature of infinity that was reproduced in Scientific American in December 2013. The dispute reported on here has to do with a choice between two systems of axioms.
According to the researchers, choosing between the candidates boils down to a question about the purpose of logical axioms and the nature of mathematics itself. Are axioms supposed to be the grains of truth that yield the most pristine mathematical universe? … Or is the point to find the most fruitful seeds of mathematical discovery…
Grains of truth or seeds of discovery, this is a fairly interesting and, I would add, unexpected choice for mathematics to have to make. The dispute in its entirety says something intriguing about us, not just about mathematics. The complexity of the questions surrounding the value and integrity of infinity, together with the history of infinite notions is well worth exploring, and I hope to do more.
By Joselle, on August 31st, 2016 Random is often the word chosen to describe something that has no order. But randomness has become an increasingly useful tool in mathematics, a discipline whose meaningfulness relies, primarily, on order.
In statistics, randomness as a measure of uncertainty, makes possible the identification of events, whether sociopolitical or physical, with the use of probability distributions. We use random sampling to create tools that reduce our uncertainty about whether something has actually happened or not. In information theory, entropy quantifies uncertainty, and makes the analysis of information, in the broadest sense, possible. In algorithmic information theory randomness helps us quantify complexity. Randomness characterizes the emergence of certain kinds of fractals found in nature and even the action of organisms. It has been used to explore neural networks, both natural and artificial. Researchers, for example, have explored the use of a chaotic system in a machine that might then have properties important to brain-like learning, adaptability and flexibility. Gregory Chaitin’s metabiology, outlined in his book Proving Darwin: Making Biology Mathematical, investigates the random evolution of artificial software that might provide insight into the random evolution of natural software (DNA).
Quanta Magazine recently published a piece with the title, A Unified Theory of Randomness, in which Kevin Hartnett describes the work of MIT professor of mathematics Scott Sheffield, who investigates the properties of shapes that are created by random processes. These are shapes that occur naturally in the world but, until now, appeared to have only their randomness in common.
Yet in work over the past few years, Sheffield and his frequent collaborator, Jason Miller, a professor at the University of Cambridge, have shown that these random shapes can be categorized into various classes, that these classes have distinct properties of their own, and that some kinds of random objects have surprisingly clear connections with other kinds of random objects. Their work forms the beginning of a unified theory of geometric randomness.
“You take the most natural objects — trees, paths, surfaces — and you show they’re all related to each other,” Sheffield said. “And once you have these relationships, you can prove all sorts of new theorems you couldn’t prove before.”
In the coming months, Sheffield and Miller will publish the final part of a three-paper series that for the first time provides a comprehensive view of random two-dimensional surfaces — an achievement not unlike the Euclidean mapping of the plane.
The article is fairly thorough in making the meaning of these advances accessible. But with limited time and space, I’ll just highlight a few things:
In this ‘random geometry,’ if the location of some of the points of a randomly generated object are known, probabilities are assigned to subsequent points. As it turns out, certain probability measures arise in many different contexts. This contributes to the identification of classes and properties, critical to growth in mathematics.
We can all imagine random motion, or random paths, but here the random surface is explored. As Hartnett tells us,
Brownian motion is the “scaling limit” of random walks — if you consider a random walk where each step size is very small, and the amount of time between steps is also very small, these random paths look more and more like Brownian motion. It’s the shape that almost all random walks converge to over time.
Two-dimensional random spaces, in contrast, first preoccupied physicists as they tried to understand the structure of the universe.
Sheffield was interested in finding a Brownian motion for surfaces. And two ideas that already existed would help lead him. Physicists have a way of describing a random surface, whose surface area could be determined (related to quantum gravity). There is also something called a Brownian map, whose structure allows the calculation of distance between points. But the two could not be shown to be related. If there was a way to measure distance on former structure, it could be compared to distances measured on the latter. Their hunch was that these two surfaces were different perspectives on the same object. To overcome the difficulty of distance measurement on the former, they used growth over time as a distance metric.
…as Sheffield and Miller were soon to learn, “[random growth] becomes easier to understand on a random surface than on a smooth surface,” said Sheffield. The randomness in the growth model speaks, in a sense, the same language as the randomness on the surface on which the growth model proceeds. “You add a crazy growth model on a crazy surface, but somehow in some ways it actually makes your life better,” he said.
But they needed another trick to model growth on very random surfaces in order to establish a distance structure equivalent to the one on the (very random) Brownian map. They found it in a curve.
Sheffield and Miller’s clever trick is based on a special type of random one-dimensional curve that is similar to the random walk except that it never crosses itself. Physicists had encountered these kinds of curves for a long time in situations where, for instance, they were studying the boundary between clusters of particles with positive and negative spin (the boundary line between the clusters of particles is a one-dimensional path that never crosses itself and takes shape randomly). They knew these kinds of random, noncrossing paths occurred in nature, just as Robert Brown had observed that random crossing paths occurred in nature, but they didn’t know how to think about them in any kind of precise way. In 1999 Oded Schramm, who at the time was at Microsoft Research in Redmond, Washington, introduced the SLE curve (for Schramm-Loewner evolution) as the canonical noncrossing random curve.
Popular opinion often finds fault in attempts to quantify everything, as if quantification is necessarily diminishing of things. What strikes me today is that quantification is more the means to finding structure. But it is the integrity of those structures that consistently unearths surprises. The work described here is a beautiful blend of ideas that bring new depth to the value of geometric perspectives.
“It’s like you’re in a mountain with three different caves. One has iron, one has gold, one has copper — suddenly you find a way to link all three of these caves together,” said Sheffield. “Now you have all these different elements you can build things with and can combine them to produce all sorts of things you couldn’t build before.”
By Joselle, on June 30th, 2016 First, I would like to apologize for posting so infrequently these past few months. I have been working hard to flesh out a book proposal closely related to the perspective of this blog, and I will be focused on this project for a bit longer.
However, a TED talk filmed in Paris in May came to my attention today. The talk was given by Blaise Agüera y Arcas who works on machine learning at Google. It was centered on illustrating the intimate connection between perception and creativity. Agüera y Arcas surveyed the history of neuroscience a bit, as well as the birth of machine learning, and the significance of neural networks. This was the message that caught my attention.
In this captivating demo, he shows how neural nets trained to recognize images can be run in reverse, to generate them.
There must be a significant insight here. The images produced when neural nets are run in reverse are very interesting. They are full of unexpected yet familiar abstractions. One of the things I found particularly interesting, however, was how Agüera y Arcas described the reversal of the recognition process. He first drew us a picture of a neural network involved in recognizing or naming an image, specifically, a first layer of neurons (pixels in an image or neurons in the retina) that feed forward to subsequent layers, connected by synapses with varying strengths, that govern the computations that end in the identification or the word for the image. He then suggested representing those things – the input pixels, the synapses, and the final identification – with three variables x, w, and y respectively. He reminded us, there could be a million x values, billions or trillions of w values and a small number of y values. But put in relationship, they resemble an equation with one unknown (namely the y) – the name of the object to be found. If x and y are known, finding w is a learning process:
So this process of learning, of solving for w, if we were doing this with the simple equation in which we think about these as numbers, we know exactly how to do that: 6 = 2 x w, well, we divide by two and we’re done. The problem is with this operator. So, division — we’ve used division because it’s the inverse to multiplication, but as I’ve just said, the multiplication is a bit of a lie here. This is a very, very complicated, very non-linear operation; it has no inverse. So we have to figure out a way to solve the equation without a division operator. And the way to do that is fairly straightforward. You just say, let’s play a little algebra trick, and move the six over to the right-hand side of the equation. Now, we’re still using multiplication. And that zero — let’s think about it as an error. In other words, if we’ve solved for w the right way, then the error will be zero. And if we haven’t gotten it quite right, the error will be greater than zero.
So now we can just take guesses to minimize the error, and that’s the sort of thing computers are very good at. So you’ve taken an initial guess: what if w = 0? Well, then the error is 6. What if w = 1? The error is 4. And then the computer can sort of play Marco Polo, and drive down the error close to zero. As it does that, it’s getting successive approximations to w. Typically, it never quite gets there, but after about a dozen steps, we’re up to w = 2.999, which is close enough. And this is the learning process.
…It’s exactly the same way that we do our own learning. We have many, many images as babies and we get told, “This is a bird; this is not a bird.” And over time, through iteration, we solve for w, we solve for those neural connections.
The interesting thing happens when you solve for x.
And about a year ago, Alex Mordvintsev, on our team, decided to experiment with what happens if we try solving for x, given a known w and a known y. In other words, you know that it’s a bird, and you already have your neural network that you’ve trained on birds, but what is the picture of a bird? It turns out that by using exactly the same error-minimization procedure, one can do that with the network trained to recognize birds, and the result turns out to be … a picture of birds. So this is a picture of birds generated entirely by a neural network that was trained to recognize birds, just by solving for x rather than solving for y, and doing that iteratively.
All of the images displayed are really interesting. And there are multilayered references to mathematics here: the design of neural networks, conceptualizing and illustrating what it means to ‘run in reverse,’ and even the form the abstractions take in the images produced (which are shown in the talk). Many of the images are Escher-like. It’s definitely worth a look.
In the end, Agüera y Arcas makes the point that computing, fundamentally, has always involved modeling our minds in some way. And the extraordinary progress that has been made in computing power and machine intelligence “gives us both the ability to understand our own minds better and to extend them.” In this effort we get a fairly specific view of what seems to be one of the elements of creativity. This will continue to highlight the significance of mathematics in our ongoing quest to understand ourselves.
|
|

![]()

 The geometrically defined proportions of the human body, for example, produced by Roman architect and engineer Marcus Vitruvius Pollio in the 1st century BC, and explored again by Leonardo da Vinci in the 15th century, are displayed in the floor plans of Florence Cathedral, as well as Reims Cathedral and Milan Cathedral. These same proportions are also found in the facades of Notre-Dame of Laon, Notre-Dame of Paris, and Amiens Cathedrals. Natural spirals that reflect the Fibonacci series can be seen in patterns that are found in San Marco, Venice, the windows of Chartres Cathedral, as well as those in San Francesco d’Assissi in Palermo, and in the carving on the pulpit of Strasburg Cathedral.
The geometrically defined proportions of the human body, for example, produced by Roman architect and engineer Marcus Vitruvius Pollio in the 1st century BC, and explored again by Leonardo da Vinci in the 15th century, are displayed in the floor plans of Florence Cathedral, as well as Reims Cathedral and Milan Cathedral. These same proportions are also found in the facades of Notre-Dame of Laon, Notre-Dame of Paris, and Amiens Cathedrals. Natural spirals that reflect the Fibonacci series can be seen in patterns that are found in San Marco, Venice, the windows of Chartres Cathedral, as well as those in San Francesco d’Assissi in Palermo, and in the carving on the pulpit of Strasburg Cathedral. Vesica Pisces was the name given to the figure created by the intersection of two circles with the same radius in such a way that the center of each circle is on the perimeter of the other. A figure thus created has some interesting geometric properties, and was often used as a proportioning system in Gothic architecture. It can be found in the working lines of pointed arches, the plans of Beauvais Cathedral and Glastonbury Cathedral, and the facade of Amiens Cathedral. Fractal patterns are also seen in windows of Amiens, Milan, Chartres Cathedrals and Sainte-Chapelle, Paris. And the shapes of Gothic vaults are shown to reflect variations of fractal trees in Wales Cathedral, the Church of Hieronymite Monastery, Portugal, Frauenkirche, Munich and Gloucester Cathedral.
Vesica Pisces was the name given to the figure created by the intersection of two circles with the same radius in such a way that the center of each circle is on the perimeter of the other. A figure thus created has some interesting geometric properties, and was often used as a proportioning system in Gothic architecture. It can be found in the working lines of pointed arches, the plans of Beauvais Cathedral and Glastonbury Cathedral, and the facade of Amiens Cathedral. Fractal patterns are also seen in windows of Amiens, Milan, Chartres Cathedrals and Sainte-Chapelle, Paris. And the shapes of Gothic vaults are shown to reflect variations of fractal trees in Wales Cathedral, the Church of Hieronymite Monastery, Portugal, Frauenkirche, Munich and Gloucester Cathedral.


Recent Comments